Пусть в результате дискретизации получена непрерывная последовательность отсчетов Х (nDt). Для передачи по цифровому каналу связи каждый отсчет квантуется до конечного множества значений.
Этапы процесса представления сообщений:
1. Дискретизация
2. Квантование
3. Кодирование
Обычно для кодирования квантованных отсчетов используется двоичная последовательность. С помощью В - разрядного кодового слова можно представить ![]() уровней.
уровней.
Определим, как зависит отношение с/ш квантователя от В:
пусть ![]()
![]()
Динамический диапазон
![]()
![]()
где е (n) - шум квантования е (n) £ d/2
Модель шумов квантования:
1. шум квантования - стационарный белый шум
2. шум квантования некоррелирован с входным сигналом
3. распределение шума квантования равномерное в пределах d/2
![]()
считаем, что ![]() (сигнал согласован с апертурой квантователя)
(сигнал согласован с апертурой квантователя)
следовательно: ![]()
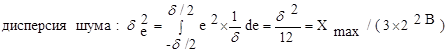
получаем: ![]() (2.1)
(2.1)
Определим отношение с/ш (q), при котором достигается вероятность ошибки на символ Рош=10-6.
Кодирование сообщений в радиосистемах может быть использовано для повышения:
1) достоверности принятых сообщений,
2) помехоустойчивости радиолиний с целью снижения мощности передатчика. Кодирование сообщений для указанных целей называется помехоустойчивым, в отличие от других видов кодирования, применяемых для решения задач (формирования адресов, сигналов синхронизации и др.), а также при устранении избыточности сигналов источников сообщений.
Пусть цифровое сообщение кодируется двоичным (n,k) - кодом, где n - общее число символов, k - число информационных символов.
Эквивалентная вероятность ошибки:
рэ= (dx Mбл /2n) , (2.2)
где Еб/N0=Pcto/N0; Еб - энергия сигнала, затрачиваемая на один бит информации; Pc - мощность принимаемого сигнала; to - длительность одного информационного символа, поступающего на вход кодера канала связи; dx - кодовое расстояние между рассматриваемыми символами; Mбл - число ближайших сигналов на расстоянии d от принимаемого сигнала; N0 - спектральная плотность белого шума. Интеграл вероятности можно аппроксимировать экспоненциальной функцией. В широкой области значений р<<1 вероятность ошибки хорошо аппроксимируется выражением
p=0,5 Тогда из (2.3) получим
рэ= (dxMбл/10n) exp (-Eбdxk/nN0).
Отсюда Ln (10рэ) =Ln (dxMбл/n) - Eбdxk/nN0 или
Еб/N0= (Ln (dxMбл/n) - Ln (10рэ)) /dx (k/n). Перейти на страницу: 1 2
Другое по теме:
Диктофон В настоящее время до девяноста процентов всего потока информации воспринимается органами зрения человека. Поэтому важным направлением научной организации труда является увеличение части потока информации, воспринимаемой другими органами чувств и ...