Используя известное тригонометрическое равенство, называемое теоремой Эйлера, введем комплексную запись синусоидальной несущей
(6.4)
Во-первых, при комплексной записи в компактной форме, 
указаны два важных компонента любой синусоидальной несущей волны, называемых взаимно ортогональными синфазной (действительной) и квадратурной (мнимой) составляющими. Во-вторых, как показано на рисунке 6.1, не модулированная несущая удобно представляется в полярной системе координат в виде единичного вектора с постоянной скоростью рад/с, вращающегося против часовой стрелки.
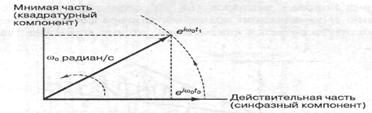
Рисунок 6.1 - Векторное представление синусоиды
При увеличении t (от t0 до t1 мы можем изобразить переменные во времени проекции вращающегося вектора на синфазной (l) и квадратурной (Q) осях. Эти декартовы оси обычно называются синфазным (l channel) и квадратурным каналом (Q channel), а их проекции представляют взаимно ортогональные составляющие сигнала, связанные с этими каналами. В-третьих, процесс модуляции несущей можно рассматривать как возмущение вращающегося вектора (и его проекций).
Рассмотрим, например, несущую, амтитудно-модулированную синусоидой с единичной амплитудой и частотой ωm, где ωm ≤ω0. Переданный сигнал имеет следующий вид.
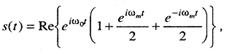(6.5)
где Re{x} - действительная часть комплексной величины На рисунке 6.2 показано, что вращающийся вектор , представленный на рисунке 6.1, возмущается двумя боковыми членами - 
, вращающимся против часовой стрелки, и 
, вращающимся по часовой стрелке. Боковые векторы вращаются намного медленнее, чем вектор несущей волны. В результате модулированный вращающийся вектор несущей волны растет и уменьшается согласно указаниям боковых полос, но частота его вращения остается постоянной; отсюда и название - "амплитудная модуляция".
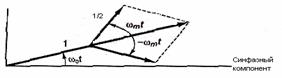
Рисунок 6.2 - Амплитудная модуляция
Еще один пример, иллюстрирующий полезность векторного представления, - это частотная модуляция (frequency modulation - FM) несущей похожей синусоидой частотой вращения ωm рад/с. Аналитическое представление узкополосной частотной модуляции (narrowband FM - NFM) подобно представлению амплитудной модуляции и описывается выражением:
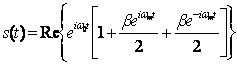
(6.6)
где β - коэффициент модуляции. На рисунке 6.3 показано, что, как и в предыдущем случае, вектор несущей волны возмущается двумя боковыми векторами. Но поскольку один из них, как указано в формуле (6.6), имеет знак "минус", симметрия боковых векторов, вращающихся по часовой стрелке и против нее, отличается от имеющегося случая амплитудной модуляции. При модуляции AM симметрия приводит к увеличению и уменьшению вектора несущей волны со временем. В случае модуляции NF> симметрия боковых векторов (на 90° отличающаяся от симметрии AM) приводит к ускорению и замедлению вращения вектора согласно указаниям боковых полос, при этом амплитуда остается неизменной; отсюда название - "частотная модуляция".
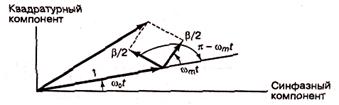
Рисунок 6.3 - Узкополосная частотная модуляция Перейти на страницу: 1 2
Другое по теме:
Проект городской телефонной станции на основе пакетной транспортной сети Существующие телекоммуникационные сети обладают целом рядом недостатков, из которых следует отметить их узкую специализацию, отсутствие гибкости и адаптации к изменению требований пользователей, а также низкую эффективность использования сетевых ...