Для уменьшения собственных шумов и для того, чтобы фильтры были всегда устойчивы, рассчитаем их на основе КИХ-фильтров. Воспользуемся методом окон. Для этого сначала рассчитаем импульсную характеристику ФНЧ по известной частотной.
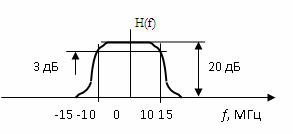
Рисунок 2 - Требуемая передаточная функция
Нормируем частоту по правилу 
, где Т-период дискретизации, и запишем передаточную характеристику следующим образом:
Найдем коэффициенты импульсной характеристики идеального ФНЧ:
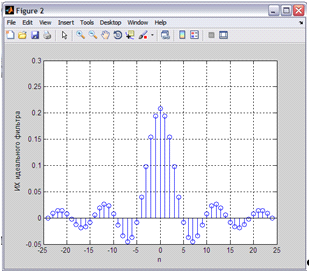
Рисунок 3 - Требуемая импульсная характеристика ФНЧ
Воспользуемся окном Кайзера, так как оно является одним из наиболее оптимальных окон и позволяет учитывать заданное ослабление в полосе пропускания и задержания. Его импульсная характеристика имеет вид:
где I0(x)- функция Бесселя нулевого порядка, β - коэффициент определяющий долю энергии, сосредоточенной в главном лепестке спектра оконной функции, N - порядок фильтра.
- заданное ослабление в полосе пропускания.
Порядок фильтра определяется следующим соотношением:
∆=N*∆
(8)
С учётом того, что а=20, ∆=5/120≈0.0416, получаем β=0, N≈23.
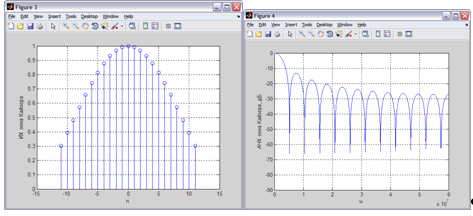
Рисунок 4 - ИХ окна Кайзера Рисунок 5 - АЧХ окна Кайзера
Импульсная характеристика искомого КИХ-фильтра получается перемножение весовой функции окна и импульсной характеристики идеального фильтра:
h(n)=hи(n)wК(n) (10)
где hи(n)- ИХ идеального ФНЧ, wК(n) - ИХ окна Кайзера.
Построим ИХ и АЧХ реального фильтра при помощи Matlab при N=23.
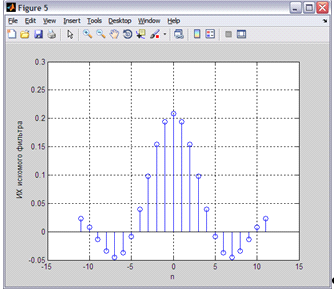
Рисунок 6 - ИХ полученного фильтра при N=23
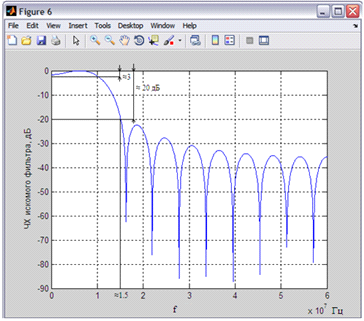
Рисунок 7 - АЧХ полученного фильтра при N=23
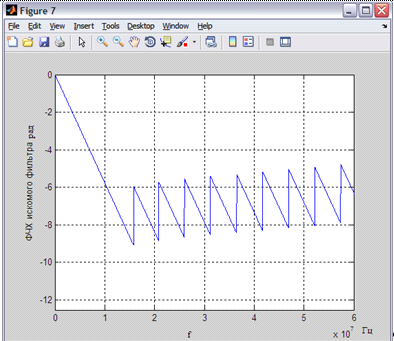
Рисунок 8 - ФЧХ полученного фильтра
Покажем теперь, что при меньшем N требования не удовлетворяются.
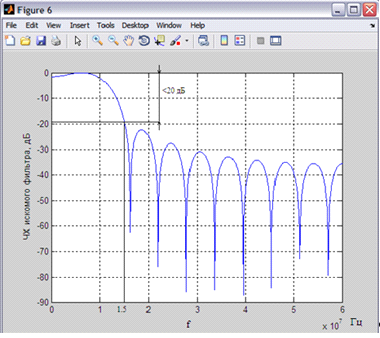
Рисунок 9 - АЧХ полученного фильтра при N=21
Как видим из рисунка 9, при меньшем N не удовлетворяется требование по величине ослабления в полосе задержания, поэтому оптимальный порядок фильтра N=23.
Другое по теме:
Технико-экономический проект развития СТС Монтированная емкость станций, № АТС – 1 150 АТС – 2 50 АТС – 3 150 АТС – 4 50 АТС – 5 50 ...