
Считается, что для работы системы необходим один работающий элемента. При выходе из строя рабочего элемента системы и при наличии элемента, находящегося в теплом резерве, этот элемент переводится в рабочее состояние.
Граф состояний системы

Рабочими для системы являются состояния с 0 по 2, состоянием отказа системы является состояние 3.
Расчет основных характеристик системы
Система дифференциальных уравнений, соответствующая графу состояний системы, имеет вид:
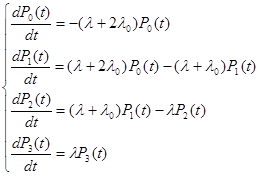
Нормировочное условие: ![]()
Начальные условия для системы дифференциальных уравнений:
P0(0)=1
P1(0)=0
P2(0)=0
P3(0)=0
При расчете методом дифференциальных уравнений, после применения прямого преобразования Лапласа при начальных условиях система примет вид:
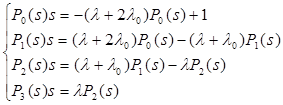
Из этой системы получим Рi(t):
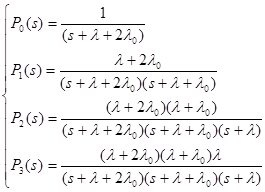
После применения обратного преобразования Лапласа система примет вид:
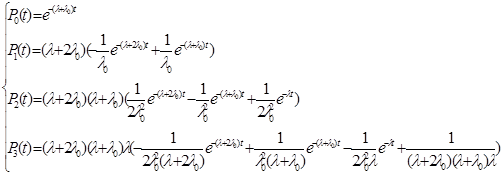
Вероятность безотказной работы системы
Функцию вероятности нахождения системы в рабочем состоянии, в силу наличия одного состояния отказа и нормировочного условия, можно записать следующим образом:
сист = P0(t)+P1(t)+P2(t) = 1-P3(t)
Для заданных значений t = 4 ч, ![]() = 0.8 1/ч и
= 0.8 1/ч и ![]() 0 = 0.4 1/ч Pсист = 0.184.
0 = 0.4 1/ч Pсист = 0.184.
Зависимость вероятности безотказной работы P(t) от времени работы для разных значений интенсивности отказа резервных элементов λ0 представлена на графике:
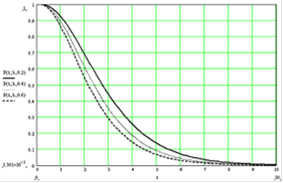
Среднее время безотказной работы
Среднее время безотказной работы рассчитывается по формуле:
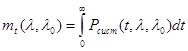
Для заданного значения λ=0.8 1/ч и λ0=0.4 1/ч среднее время безотказной работы mt = 2.708ч.
1. Вероятность безотказной работы системы изменяется по экспоненциальному закону с течением времени.
. При увеличении времени работы системы вероятность ее безотказной работы уменьшается.
. При увеличении интенсивности отказов нагруженных элементов l вероятность безотказной работы системы за один и тот же промежуток времени уменьшается.
. При увеличении интенсивности отказов частично нагруженных элементов l0 вероятность безотказной работы системы за один и тот же промежуток времени уменьшается.
. При увеличении интенсивности отказов нагруженных элементов l среднее время безотказной работы уменьшается.
. При увеличении интенсивности отказов частично нагруженных элементов l0 среднее время безотказной работы уменьшается.
. Для заданных значений интенсивностей отказов λ = 0.8 1/ч, λ0 = 0.4 1/ч и времени t = 4 ч вероятность безотказной работы системы Pсист = 0.184.
. Для заданных значений интенсивностей отказов λ = 0.8 1/ч и λ0 = 0.4 1/ч среднее время безотказной работы mt составляет 2.708 ч, что ниже заданного t = 4 ч. Т.о. с вероятностью 0.184 к заданному времени система будет находится в работоспособном состоянии.