Одной из главных целей синтеза автоматической системы является обеспечение требуемой точности в установившихся и переходных режимах. Точность систем в установившихся режимах можно улучшить, увеличивая порядок астатизма и коэффициент разомкнутого контура. Но при этом, как правило, уменьшается запас устойчивости, увеличивается колебательность и, как следствие, ухудшается точность системы в переходных процессах. Эффективным средством устранения противоречия между условиями точности в установившихся и переходных режимах служит компенсация внешних воздействий путём осуществления инвариантности (независимости одной физической величины от другой).
Инвариантность в автоматических системах достигается при помощи управления по возмущению: управляющее воздействие формируется в зависимости от изменений возмущающего воздействия.
Рассмотрим схему комбинированной системы (рис. 1). Уравнение такой системы имеет вид:
+
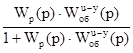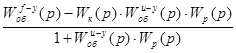, (6.1)
где:
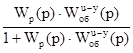- передаточная функция системы по задающему воздействию;
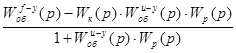- передаточная функция системы по возмущению.
Управляемая величина не зависит от возмущения, если передаточная функция по возмущению равна нулю. А это возможно, если равен нулю её числитель. Отсюда условие инвариантности стабилизируемой величины по отношению к возмущению:
.
Находим передаточную функцию компенсирующего устройства:
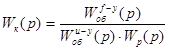. (6.2)
Подставляя в формулу (6.2) найденные ранее передаточные функции объекта по различным каналам и регулятора, получаем передаточную функцию компенсирующего устройства:
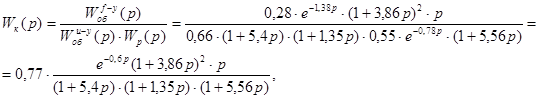
где запаздывание можно разложить следующим образом:
(6.3)
Для удобства практической реализации компенсатора используется типовой физически реализуемый компенсатор, передаточная функция которого имеет вид:
(6.4)
Вопрос при этом сводится к поиску таких k1 и Тк, при которых выражение (6.4) максимально приближается к (6.3). Делается это по следующим формулам:
,
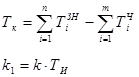где k - коэффициент усиления в формуле (6.3)
Ти - постоянная времени регулятора
По формулам разложения дробно-рациональных функций:
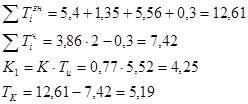
Полученная передаточная функция физически реализуемого компенсатора имеет вид:
Другое по теме:
Обнаружение многопозиционного сигнала Баркера на фоне гауссовского шума Настоящая курсовая работа завершает изучение дисциплины "Основы компьютерного проектирования и моделирования РЭС". Цель проектирования – приобретение студентами первого опыта самостоятельной разработки радиотехнической системы с помощь ...