Одним из ценнейших функциональных преимуществ НЦУ является возможность точной реализации алгоритмов управления любой сложности. Однако в настоящее время большинство систем НЦУ являются цифровыми копиями традиционных аналоговых систем, поэтому все реальные системы НЦУ базируются на применении классических ПИ- и ПИД-алгоритмов управления.
Система автоматического регулирования с НЦУ (рис. 5) содержит объект управления и автоматический регулятор (очерчен штриховой линией). Роль последнего выполняет ЭВМ снабжённая рядом устройств, для преобразования сигналов из аналоговой формы в цифровую (АЦП), а также из цифровой формы в аналоговую (ЦАП). На рисунке 5 аналоговые сигналы обозначены как функции времени y(t), g(t), z(t). Соответствующие цифровые сигналы отличаются от них не только формой представления величин, но и дискретным характером изменения во времени. Изменения значений цифровых сигналов производится в моменты времени 
где Тд - интервал дискретности; i = 0, 1, 2, …
Цифровые сигналы обозначены на схеме как переменные с индексами y, g, z, причём y = y(nTд); g = g(nТд); z = z(nТд). Интервал дискретности Тд выбирается из условия: Тд £Ти.0,1, где Ти - постоянная времени интегрирования непрерывного регулятора. В нашем случае: Тд = 5,52/10 = 0,552 с.
Рис. 5. Структурная схема системы НЦУ
Алгоритм работы ЭВМ, осуществляющий автоматическое регулирование, может быть получен из уже найденного закона регулирования непрерывного регулятора.
Принимаем за исходный ПИ-закон:
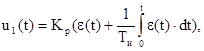(8.1)
где:1(t) - регулирующее воздействие на объект;
e(t) - сигнал ошибки,
e(t) = g(t) - y(t); Кр и Ти - параметры настройки непрерывного ПИ-регулятора.
Замена непрерывных сигналов цифровыми, взятыми в дискретные моменты, может быть проведена по следующей схеме:
e(t) ® e; u1(t) ® u1;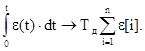 
Здесь и ниже для удобства записи принимаем:
u=u; 
ПИ-закон регулирования в цифровой форме имеет вид:
(8.2)
Более удобна для реализации на ЭВМ другая, так называемая скоростная форма этого алгоритма. Для её получения запишем значение u1 на предыдущем интервале дискретности:
Вычитая его из предыдущего, получим:
Отсюда:
После подстановки e = g - y; e = g - y получим:
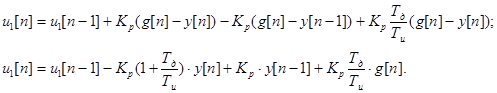
Подставив значения всех постоянных коэффициентов, получим:
(8.3)
Алгоритм работы ЭВМ, осуществляющий компенсацию возмущающего воздействия, может быть получен на основании передаточной функции компенсатора следующим образом.
Пусть, например, сигнал компенсатора u2(t) подаётся на вход объекта (вместе с сигналом регулирования u1) и пусть передаточная функция компенсатора:
. (8.4)
Тогда соответствующее операторное выражение имеет вид:
и в дифференциальной форме записывается в виде:
Переход к цифровым сигналам, взятым в дискретные моменты времени, может быть проведён по следующей схеме:
В результате перехода получим:
Отсюда:
.
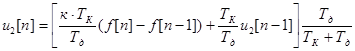Подставив значения всех постоянных коэффициентов, получим:
Перейти на страницу: 1 2
Другое по теме:
Воздушные линии электропередачи Воздушной линией электропередачи (ВЛ) называется устройство для передачи и распределения электроэнергии по проводам, расположенным на открытом воздухе и прикрепленным изоляторами и арматурой к опорам или кронштейнам инженерны ...