Необходимо рассчитать компенсирующее воздействие нечёткого компенсатора u2 для случая, когда |f| = 0,2 и |f’| = 0,1. Упрощённый алгоритм нечёткого управления представлен следующими двумя правилами:
Правило №1: Если |f| = ПБ ИЛИ |f’| = ПН, тогда Uк = ПБ;
Правило №2: Если |f| = ОБ И |f’| = ПН, тогда Uк = ПН.
Fuzzy-логика осуществляется в 3 этапа:
I этап - фаззификация.
Фаззификация осуществляет переход от четких измеренных значений f и f’ к нечеткому множеству значений входа. Этот переход осуществляется с помощью функций принадлежности. Каждому значению f ставится в соответствие определенное значение функции принадлежности. После этого начинается II этап - разработке нечетких правил.
Вычисление этих правил состоит из двух процедур: сначала рассчитывается все в части Если, а потом в части Тогда.
Посылка «ЕСЛИ», первого правила, содержащая внутри себя союз «ИЛИ» даёт значение функции принадлежности m1 (f1, f2), соответствующее логической конъюнкции:
m1 (f, f’) = max{mПБ(f), mПН(f’)} = max {0,4; 0,8} = 0,8;
m2 (f, f) = min{mОБ(f), mПН(f’)} = min {0,4; 0,2} = 0,2.
Теперь в соответствии с композиционным правилом Мамдани:
mjn (x, uj) = min{mj(x), m1(uj)} (6.1)
где mjn (x, uj) - ФП, характеризующая i - лингвистическое значение управляющего воздействия u в j - правиле;
x - вектор входных переменных.
Можно определить результирующие функции принадлежности, характеризующие импликации правил 1 и 2 (приложение 5.), где miU2 - функции принадлежности, характеризующие фаззи-множества управляющих воздействий u. Так как функции m1,2 (f1, f2) принимают конкретные значения, меньшие единицы, то результатам импликации соответствуют «усечённые» функции принадлежности miU2 (приложение5).
Выполняя процедуру фаззи-объединения функций miU2 (агрегирование) получаем результирующую функцию принадлежности m*(U2) (приложение 5).
Заключительным этапом Fuzzy-логики является дефаззификация, которая сводится к определению точного значения управляющего воздействия u
по нечеткому множеству. Она выполняется чаще всего по методу центра тяжести, согласно которому для непрерывной функции искомое значение управляющего воздействия определяется как абсцисса центра тяжести площади фигуры, образованной этой функцией и осью u.
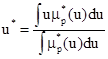 .
.
На практике широко используется упрощённая формула, в которой интеграл заменяется суммой, т.е.
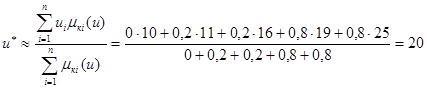
где ui - абсцисса среднего (центрального) значения выходного множества (управляющих воздействий);
mpi(u) - функция принадлежности - высота отсечения - выходного множества (управляющих воздействий).
В данной работе выполнен синтез комбинированной САУ техническим объектом, заданным в форме экспериментальных переходных характеристик. Произведен выбор математической модели объекта управления в форме передаточных функций по управляющему и возмущающему каналам, выбран ПИ алгоритм управления и произведен расчет параметров ПИ-регулятора графоаналитическим методом. Рассчитан физически реализуемый компенсатор, обеспечивающий компенсацию возмущений. Построены кривые переходных процессов в системе и определены показатели качества. Осуществлен переход од аналогового (непрерывного) регулятора к НЦУ. Построена САУ с использованием методов нечёткой логики. Рассчитано компенсирующее воздействие нечёткого компенсатора.
Другое по теме:
Методы расчета БИХ-фильтров Цифровые системы - это системы с цифровыми сигналами на входе и выходе. Их ядром обычно является ЦВМ. Человечество создало мало объектов, имеющих цифровую природу, поэтому общий термин цифровая система применяется редко. Гораздо чаще встречаются ...