цифровой код баркер гауссовский шум
Согласованный (оптимальный) фильтр максимизирует отношение сигнал/шум на своём выходе. Структура СФ в общем случае определяется сигналом Баркера u(t) и вероятностными характеристиками шума n(t). Так, если на входе СФ действует аддитивная смесь: x(t)=u(t)+n(t), где n(t) - гауссовский белый шум, то комплексный коэффициент передачи G(jω) и импульсная характеристика g(t) фильтра имеют вид :
G(jω)=kU*(jω)еxp(-jωt0)
g(t)=ku(t0-t)
Здесь U*(jω) - комплексно-сопряженная спектральная плотность сигнала u(t);
k -коэффициент усиления СФ, задаваемый произвольно;
t0 -временная задержка фильтра, определяемая из условия физической реализуемости:
g(t)=0, t<0 (5.1.)
Условие (5.1.) означает, что отклик фильтра на произвольное входное воздействие не может появиться раньше этого воздействия. Обычно выбирают t0=Т=Nτ - длительность сигнала u(t). Рассмотрим некоторые свойства CФ.
1 - Сигнал на выходе фильтра, согласованного с входным сигналом u(t), совпадает по форме с автокорреляционной функцией (АКФ) этого сигнала, сдвинутой по оси времени на величину t0. Это непосредственно следует из подстановки импульсной характеристики и сигнала u(t) в интеграл Дюамеля, связывающего выходной сигнал с импульсной характеристикой g(t) и входным сигналом u(t). Таким образом, выходной сигнал в момент t=t0 имеет максимум, пропорциональный энергии входного сигнала u(t).
2 - Импульсная характеристика g(t) СФ при t0=0 является зеркальным отображением сигнала u(t)
Что бы синтезировать фильтр необходимо. Найти передаточную функцию СФ. Произведем это по формуле 5.2.:
![]() (5.2.)
(5.2.)
В результате получим выражение:
![]()
По передаточной функции построить принципиальную схему состоящую их линий задержек и суммирующего устройства (См. рисунок А.4).
Проанализируем схему, подключив к входу сигнал Баркера. В результате получим на выходе АКФ сигнала, сдвинутую на время задержки. Результат представлен на рисунке 14.

Рисунок 14 – Реакция СФ на подачу сигнала Баркера
Теперь можно подключить к входу СФ всю остальную модель. Получим следующие графики (см. рисунки 13 – 14)

Рисунок 16 – Сигнал на выходе СФ
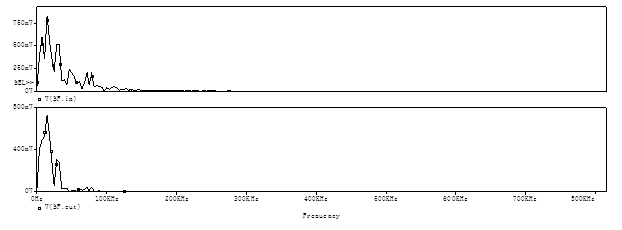
Рисунок 17 – Спектр сигнала на выходе СФ
Другое по теме:
Расчет характеристик сигналов и канала связи На современном этапе развития перед железнодорожным транспортом стоят задачи по увеличению пропускной и провозной способности, грузовых и пассажирских перевозок, уменьшению времени оборотов вагонов и повышению производительности труда. Эти зада ...