При аналоговых методах обработки для компенсации нелинейности измерительных преобразователей использовались различные электронные компоненты, работающие на нелинейных участках своих характеристик: лампы, диоды, транзисторы. Таким способом удавалось уменьшить нелинейность в полтора-два раза. Линеаризация проводилась для усредненных характеристик, подстройка для конкретных экземпляров преобразователей была сложна. Поэтому нелинейность измерительных преобразователей являлась основным фактором, ограничивавшим их точность. Ситуация принципиально изменилась с использованием для линеаризации цифровых устройств.
Применяются два основных алгоритма линеаризации:
- аппроксимация характеристики преобразования полиномом (степенным, гармоническим и др.);
- кусочно-линейная аппроксимация.
Оба метода эффективно устраняют нелинейность, если характеристика изменяется достаточно плавно (вторая производная меняет знак в рабочем диапазоне малое число раз). Нелинейность, обусловленная физическими эффектами, заложенными в принцип работы преобразователя, имеет именно такой плавный характер. Неплавная нелинейность обусловлена особенностями конструкции и качеством изготовления. Например, дефекты намотки катушек индуктивных преобразователей приводят к неплавной нелинейности. (Интервал перемещений, в пределах которого происходит изменение знака второй производной, близок к величине шага намотки, то есть составляет несколько сотых долей миллиметра.) Устранить такую нелинейность практически невозможно, поскольку для этого потребуются или полиномы очень высоких степеней, или очень большое число отрезков кусочно-линейной аппроксимации.
Оба метода имеют свои преимущества и недостатки. Однако более широкое применение нашел второй метод, как более простой и более эффективно устраняющий локальную нелинейность.
При первом подходе ищутся параметры функции известной формы (например, степенного полинома), при которых точки (xj; Cj) наименее удалены от этой функции.
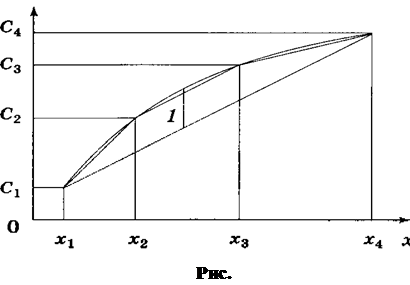

Кусочно-линейная аппроксимация (на рис. 4 длина отрезка 1 характеризует нелинейность) заключается в том, что нелинейная характеристика канала заменяется отрезками прямых, проходящих через экспериментально полученные точки (xi; Ci) и (хi + 1; Ci + l), где i = 1, п. Обычно число точек равно 6 . 11, что соответствует аппроксимации пятьюдесятью отрезками прямых.
Координаты узлов аппроксимации должны быть измерены с погрешностями, в несколько раз меньшими допускаемой погрешности ИК, аналогично тому, как это делается при калибровке или поверке.
С учетом вида аппроксимации характеристики преобразования обратное преобразование, обеспечивающее линеаризацию, также будет линейно-кусочной функцией
![]() (4)
(4)
Очевидно, что с увеличением числа линейных отрезков обеспечивается более высокая линейность. Однако при этом возрастают требуемый объем памяти (что не очень существенно) и объем экспериментальных работ по получению исходных данных.
Кусочная линеаризация позволяет уменьшить нелинейность в несколько раз и даже в десятки раз. Благодаря этому, используя датчики, конструкция которых не менялась несколько десятилетий, можно обеспечить значительно более высокую точность измерения. При этом подчеркнем, что в соответствии с рассмотренным алгоритмом производится линеаризация характеристики конкретного экземпляра датчика, а не усредненной характеристики, что устраняет и влияние разброса характеристик.
Аппаратно линеаризация может производиться центральной ЭВМ или специальными микропроцессорными устройствами, входящими в состав ИК и конструктивно объединенными с вторичными преобразователями или с АЦП. Некоторые датчики выпускаются в комплекте с ПЗУ, в котором записаны данные о его характеристике, достаточные для линеаризации. Перейти на страницу: 1 2 3
Другое по теме:
Расчет управляемого выпрямителя и СИФУ В настоящее системы преобразования переменного синусоидального напряжения и тока в постоянные практически полностью представлены полупроводниковыми выпрямителями. Очень часто также необходимо регулировать величину полученного постоянного напряже ...