Цифровой фильтр полностью описывается своим разностным уравнением:
(1)
Для нерекурсивного цифрового фильтра 
и уравнение принимает вид:
(2)
Зная коэффициенты разностного уравнения, можно легко получить выражение для передаточной функции фильтра (для НЦФ):
(3)
Для образа выходного сигнала НЦФ справедливо выражение
, (4)
где 
– z-преобразования выходного и входного сигналов фильтра.
Зная выражение (4) и учитывая, что z-преобразование функции единичного скачка 
равно 1, можно получить выражение для z-образа импульсной характеристики 
:
(5)
Из (5) следует, что отсчеты импульсной характеристики НЦФ численно равны коэффициентам разностного уравнения НЦФ, а сама импульсная характеристика и передаточная функция связаны парой z-преобразований (прямым и обратным).
Заменив в (4) z на 
, получим комплексную частотную характеристику:
(6)
Импульсная характеристика и комплексная частотная характеристика связаны парой преобразований Фурье:
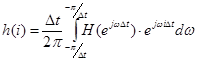(7)
(8)
Из комплексной частотной характеристики можно получить выражения для АЧХ и ФЧХ:
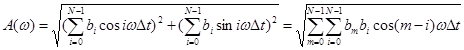(9)
(10)
Во все вышеприведённые формулы входит интервал квантования 
. Чтобы от него избавиться, частоту обычно нормируют. Это можно сделать с помощью замены:
(11)
Так как интервал определения 
, то интервал определения 
. Исходными данными для проектирования фильтра является его АЧХ. Как правило, в зонах неопределённости АЧХ некоторым образом доопределяют с тем, чтобы избежать явления Гиббса («выбросы» характеристики в точках разрыва первого рода – «скачках»). В простейшем случае доопределить АЧХ можно линейным законом. В этом случае АЧХ проектируемого полосового фильтра будет выглядеть таким образом.
Аналитически АЧХ будет записываться в виде:
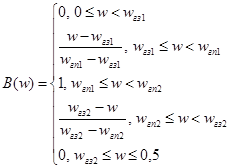(12)
При проектировании часто полагают, что ФЧХ фильтра является линейной. В показывается, что в этом случае импульсная характеристика фильтра является либо симметричной (
), либо антисимметричной (
). Учитывая, что порядок фильтра 
может быть чётным и нечётным, существует четыре вида ИХ с линейной ФЧХ:
1. N – нечётное, ИХ – симметричная
2. N – чётное, ИХ – симметричная
3. N – нечётное, ИХ – антисимметричная
4. N – чётное, ИХ – антисимметричная
цифровой фильтр выборка частотный
Другое по теме:
Суммирующий счетчик 1) Используя параметры эквивалентного логического элемента, разработанного в предыдущем КП по курсу «Компьютерное моделирование интегральных приборов», спроектировать схему триггера с динамическим управлением (фронтом или срезом синхросигнала) в ...