Находим передаточную функцию разомкнутой системы по формуле:
Wразомк. (S) = Wдп (S) * Wдв (S) * Wор (S) =
=(1,5*106*0,785*0,005)/ (10-6*S+1)(104*S+1)(0,00005*S2+10-4*S+1)=
= 5887,5/(0,00005*S2+10-4*S+1)
Находим передаточную функцию замкнутой системы по формуле:
Wзамк. (S) = Wразомк. (S) / (1 – Wразомк. (S)) =
= 5887,5/(0,00005*S2+10-4*S – 5886,5)
1. Синтез корректирующего устройства
При синтезе корректирующего устройства нужно исходить из того, что объект регулирования - неизменная часть, а синтезу подлежат корректирующие устройства или регулятор - изменяемая часть системы.
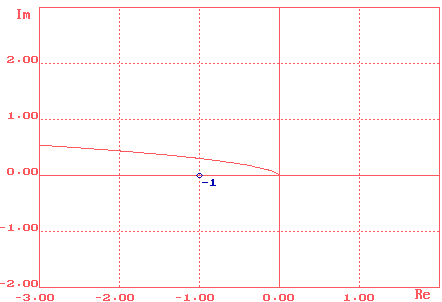
Рис.9. Годограф нескорректированной системы
При отсутствии корректирующего устройства КУ, то есть при Wку(s)=1, получены следующие характеристики:
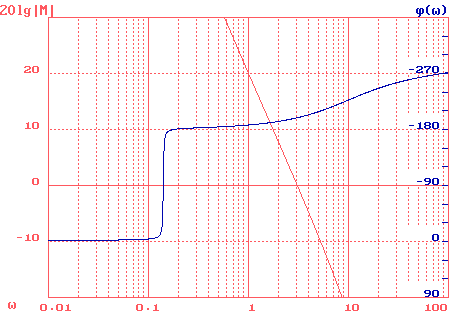
Рис.10. ЛАЧХ и ЛФЧХ нескорректированной системы
Приведённые выше характеристики были получены при общем коэффициенте усиления разомкнутой системы K, при котором должна обеспечиваться заданная точность xmax.
Так как данная система статическая , то общий коэффициент усиления разомкнутой системы определяется из соотношения:
При подстановке числовых значений получаем, что
К = 499
Об устойчивости системы можно судить по ее годографу (АФХ). В устойчивой системе кривая годографа не должна охватывать точку с координатами (-j, 0).
В данном случае полученная система неустойчива и поэтому производим расчет корректирующего устройства, используя частотный метод синтеза, основанный на построении желаемой ЛАХ.
После ввода корректирующего устройства были получены следующие характеристики:
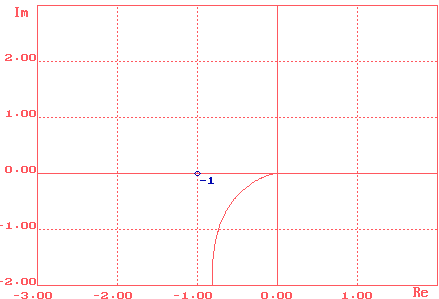
Рис.11. Годограф с КУ
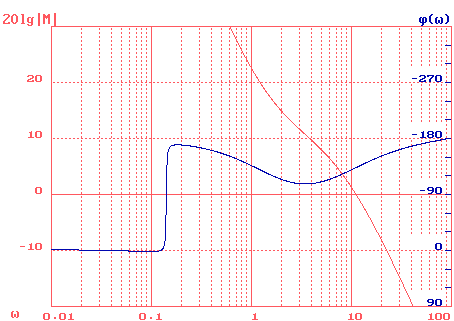
Рис.12. ЛАЧХ и ЛФЧХ с КУ
При построении характеристик (смотри рис.12) было произведено масштабирование по оси частот, то есть частота была уменьшена на три порядка (в 1000 раз).
Значит реальное корректирующее устройство имеет следующие параметры
w0 = 3090 (1/с).
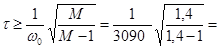0,0006054 (сек.)
= 0,0001009 (сек )
запишем передаточную функцию реального КУ:
Определяем запас устойчивости по фазе и по амплитуде (см. рис.12.):
запас устойчивости по фазе на частоте среза c равен 57°, запас устойчивости по амплитуде равен , определяемый на частоте где j(w)=-180°, 7 дб.
При задающем воздействии, равным единице (f (t) =1), процесс регулирования выглядит следующим образом (см. рис.13.).
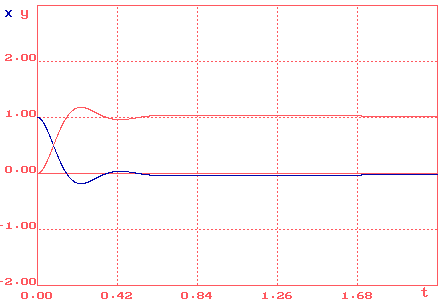
Рис.13. Процесс регулирования.
В данной курсовой работе были выполнены следующие задачи:
· Построение характеристик (годограф, ЛАЧХ и ЛФЧХ) разомкнутой системы без корректирующего устройства и с корректирующим устройством;
· Расчёт передаточных функций отдельных звеньев и передаточных функций замкнутой и разомкнутой систем;
· Расчёт общего коэффициента усиления разомкнутой системы К;
· Расчёт корректирующего устройства, определение постоянных времени: Т и t ;
По результатам курсовой работы можно сделать следующие выводы:
· При введении корректирующего устройства разомкнутая система становится устойчивой, то есть годограф не охватывает точку с координатами (-j ; 0);
· Запас устойчивости по фазе и по амплитуде лежат в пределах нормы;
· Процесс регулирования при входном синусоидальном воздействии при заданных параметрах не возможен, но возможен при
g max = 1, x max = 2 мкм, w max = 20 (1/сек.)
Другое по теме:
Делители мощности на микрополосковой линии В настоящее время область применения радиоэлектронных средств расширяется, комплексы радиосистем становятся все более сложными, это полностью относится и к радиотехнике СВЧ диапазона. В связи с расширением физических возможностей радиоэлект ...