Как уже отмечалось, абстрактный автомат работает как преобразователь слов входного алфавита в слова выходного алфавита.
Пусть абстрактный автомат Мили задан графом рис.1.5.
На вход этого автомата, установленного в начальное состояние, поступает входное слово X=x1, x1, x2, x1, x2, x2.
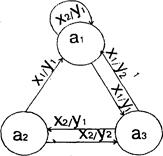
Рисунок 1.5 - Граф автомата Мили
Так как (a1, x1) = а3, a (a1, x1) = y1, то под действием первой буквы слова Х входного сигнала x1 автомат перейдет в состояние a3 и на выходе его появится сигнал y1. Далее, (а3, x1) = a1, а (а3, x1) = у2, потому при приходе второго сигнала x1 автомат окажется в состоянии a1, а на выходе его появится сигнал у2. Проследив непосредственно по графу или таблицам переходов и выходов дальнейшее поведение автомата, опишем его тремя строчками, первая из которых соответствует входному слову X, вторая - последовательности состояний, которые проходит автомат под действием букв слова X, третья - выходному слову У, которое появляется на выходе автомата:
x1
x1 x2 x1 x2 x2
a1
а3 a1
a1 а3
a2 а3
y1 y2 y1 y1 y1 y2
Назовем у = (а1, X) реакцией автомата Мили в состоянии a1 на входное слово X. Как видно из примера, в ответ на входное слово длины k автомат Мили выдает последовательность состояний длины к+1 и выходное слово длины k. В общем виде поведение автомата Мили, установленного в состояние аm, можно описать следующим образом:
| Входное слово | xi1 | xi2 | xi3 |
| Последовательность состояний | am | ai2= (am,xi1) | ai3= (ai2,xi2). |
| Выходное слово | yi1= (am,xi1) | yi2= (ai2,xi2) | yi3= (ai3,xi3) |
Точно так же можно описать поведение автомата Мура, находящегося в состоянии am, при приходе входного слова xi1, xi2,., хik. Напомним, что в соответствии с (1-2) выходной сигнал в автомате Мура в момент времени t (У (t)) зависит лишь от состояния, в котором находится автомат в момент t (a (t)):
| Входное слово | xi1 | xi2 | xi3 | |
| Последовательность состояний | am | ai2= (am,xi1) | ai3= (ai2,xi2) | ai4= (ai3,xi3) |
| Выходное слово | yi1= (am,xi1) | yi2= (ai2,xi2) | yi3= (ai3,xi3) | yi4= (ai4) |
Очевидно, что выходной сигнал уi1=λ (am) в момент времени i1 не зависит от входного сигнала xi1, а определяется только состоянием аm.
Таким образом, этот сигнал yi1 никак не связан с входным словом, поступающим на вход автомата, начиная с момента i1. В связи с этим под реакцией автомата Мура, установленного в состояние am на входное слово X=xi1, хi2,., хik будем понимать выходное слово той же длины у= λ (am,
Х) =уi2, уi3,., yik+1.
В качестве примера рассмотрим автомат Мура S5, граф которого изображен на рис.1-6, и найдем его реакцию в начальном состоянии на то же самое входное слово которое мы использовали при анализе поведения автомата Мили S1:
| Входное слово | x1 | x1 | x2 | x1 | x2 | х2 | |
| Последовательность состояний | a1 | a4 | a1 | a1 | a4 | a3 | a5 |
| Выходное слово | y1 | y1 | y2 | y1 | y1 | y1 | y2 |
Другое по теме:
Синтез системы автоматического регулирования фокусировки пятна В настоящее время оптические дисковые системы нашли множество применений. Возможность записи значительного объема информации и простота тиражирования делает оптический диск очень привлекательным. В сфере записи и хранения данных системы с прямой ...