Алгебраическими критериями называются критерии, которые основаны на проверке определенных соотношений, составленных из коэффициентов характеристического уравнения.
Поэтому при использовании алгебраических критериев нужно иметь только характеристическое уравнение вида: 
Если исследование устойчивости проводится с помощью алгебраических критериев, нужно, прежде всего, проверить выполнение необходимого условия устойчивости, так как его проверка не требует никаких вычислений и при невыполнении этого условия дальнейших исследований проводить не нужно.
Необходимое условие устойчивости. Для того чтобы система была устойчива, необходимо, чтобы коэффициенты ее характеристического уравнения были одного знака:
или 
(3)
Если необходимое условие не выполняется, то система неустойчива.
Если же необходимое условие выполняется, то система при n ³ 3 (n - порядок системы) может быть устойчивой и неустойчивой и для установления устойчивости нужно воспользоваться каким-либо критерием устойчивости. Как уже установлено, в случае систем первого и второго порядков необходимое условие (3) является и достаточным.
Перейдем к формулировке критерия Гурвица. Составим из коэффициентов характеристического уравнения определитель Гурвица п-го порядка
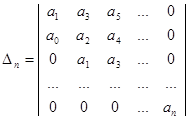
На главной диагонали к располагаются коэффициенты в порядке возрастания их индексов, начиная с 
и кончая 
. В каждом столбце при движении от элемента, находящегося на главной диагонали, вверх индексы коэффициентов возрастают, вниз – убывают. При этом на место элементов с индексами, превышающими п (при движении вверх), и отрицательными индексами (при движении вниз) проставляются нули.
Определители Гурвица – это миноры, входящие в главный определитель Гурвица
Запишем главные миноры определителя
:
, 
, 
, …
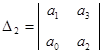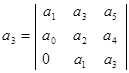Эти миноры, включая определитель
называются определителями Гурвица. Примем для определенности 
. Это допущение не нарушает общности, так как если 
, то обе части характеристического уравнения можно умножить на —1.
Критерий Гурвица. Для того чтобы система была устойчива, необходимо и достаточно, чтобы все определители Гурвица, составленные из коэффициентов ее характеристического уравнения, были больше нуля при
): 
, 
(2)
Из этого критерия следует, что при n =3 необходимое и достаточное условие устойчивости имеет вид:
, 
, 
, 
Следовательно, уже при п = 3 необходимое условие устойчивости (1) не является и достаточным. Для устойчивости систем третьего порядка кроме необходимого условия (3) должно выполняться неравенство , (т.е. разность между произведением средних коэффициентов и произведением крайних коэффициентов должна быть положительной). Перейти на страницу: 1 2
Другое по теме:
Разработка конструкции, топологии и технологического процесса изготовления интегральной микросхемы усиления тока индикации кассового аппарата Основополагающая идея микроэлектроники – конструктивная интеграция элементов схемы – приводит к интеграции конструкторских и технологических решений, при этом главной является задача обеспечения высокой надежности ИМС. Важнейшей задачей п ...