Общие сведения.
Спектр сигнала (его частотный состав) является важнейшей характеристикой сигнала. Он определяет требования к узлам аппаратуры связи - помехозащищенность, возможность уплотнения.
Спектральная плотность - это характеристика сигнала в частотной области, определяемая прямым преобразованием Фурье:
, (1.4)
где 
- временная функция сигнала;
- круговая частота
Одним из важнейших достоинств введенного интегрального преобразования Фурье является то, что решение любой практической задачи может быть перенесено с помощью спектральной плотности из временной области в частотную, и лишь на заключительном этапе расчетов результат вновь переводится во временную область с помощью обратного интегрального преобразования:
, (1.5)
Однако в данном курсовом проекте обратное преобразование не используется, задача ограничивается только поиском и анализом спектров сигналов. Для этого рассмотрено несколько свойств спектральной плотности.
Свойство вещественной и мнимой частей спектра состоит в том, что при четной функции мнимая часть 
, а при нечетной - 
. Это следует непосредственно из интегральных форм.
Свойство линейности выражается в том, что если имеется несколько сигналов
и у каждого из них имеется спектральная плотность 
, то спектральная плотность суммы сигналов равна сумме их спектральных плотностей.
Смещение сигнала во времени. Если предположить, что для сигнала спектр 
известен. Рассмотрим такой же сигнал, но возникающий с задержкой на 
. Его спектр будет равен:
, (1.6)
Частотные характеристики первого сигнала.
Спектральная плотность первого сигнала имеет следующий аналитический вид:
, (1.7)
Модуль спектральной плотности первого сигнала находится из текущего аналитического вида спектральной плотности (1.7). График модуля спектральной плотности изображен на рисунке 1.4.
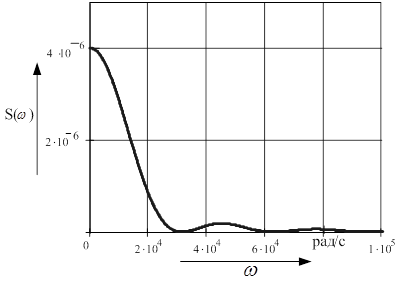
Рисунок 1.4 - Модуль спектральной плотности первого сигнала
Фаза спектральной плотности первого сигнала находится из аналитического вида спектральной плотности. Однако, из формулы спектральной плотности (1.7) следует, что 
на всей полосе частот, ввиду отсутствия мнимой составляющей.
Частотные характеристики второго сигнала.
Спектральная плотность второго сигнала имеет следующий аналитический вид:
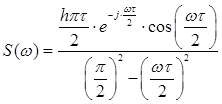, (1.8)
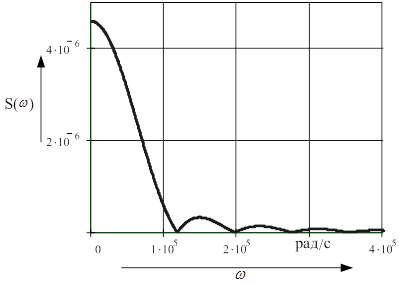
Модуль спектральной плотности второго сигнала находится из текущего аналитического вида спектральной плотности (1.8). График модуля спектральной плотности изображен на рисунке 1.5.
Перейти на страницу: 1 2
Другое по теме:
Суммирующий счетчик 1) Используя параметры эквивалентного логического элемента, разработанного в предыдущем КП по курсу «Компьютерное моделирование интегральных приборов», спроектировать схему триггера с динамическим управлением (фронтом или срезом синхросигнала) в ...