Технология цифровой связи

Затем находятся корреляции между вектором и каждым из векторов . При этом получается 8 значений корреляции, из которых составляется вектор . Из значений длительности импульса сигнала получен вектор путем умножения времени на номер строки, начиная с 0. Вектора и сведены в таблицу 3.2. Полученный результат есть табличный способ представления функции автокорреляции.

Таблица 3.2 - Табличный способ представления функции автокорреляции

01,25·10-52,5·10-53,75·10-55·10-56,25·10-57,5·10-58,75·10-510·10-511,25·10-5
10,111-0,244-0,422-0,0670,4670,111-0,244-0,244-0,067

При помощи встроенных функций вычислительной среды MathCAD можно получить также и графическое представление функции автокорреляции. Для этого сначала нужно составить вектор вторых производных для приближения к кубическому полиному при помощи векторов и взятых из таблицы 3.2.

, (3.1)

Затем составляется функция, аппроксимирующая автокорреляционную функцию кубическим сплайн-полиномом:

, (3.2)

Полученный график аппроксимирующего полинома изображен на рисунке 3.1.

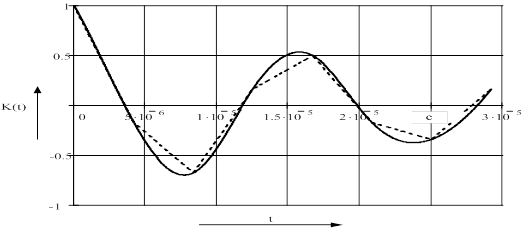
Рисунок 3.1 - АКФ, представленная в виде полиномиальной аппроксимации

.3 Спектр сигнала ИКМ

Расчет энергетического спектра кодового сигнала осуществляется с помощью интегрального преобразования Винера-Хинчена:

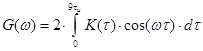, (3.3)

Полученный график энергетического спектра кодового сигнала изображен на рисунке 3.2.

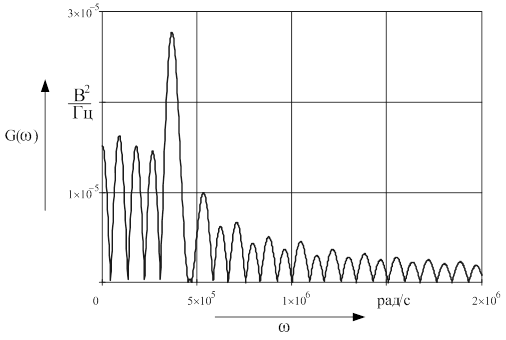
Рисунок 3.2 - Энергетический спектр кодового сигнала Перейти на страницу: 1 2 

Другое по теме:

Качество линейных непрерывных САУ и методы их оценки 310181 замкнутый линейный квадратичная интегральная ошибка Устойчивость является необходимым, но недостаточным условием работоспособности САУ. К ним предъявляют определенные требования качества. Наиболее полной характеристикой качества систем ...