Технология цифровой связи

Коэффициент готовности

Нахождение коэффициента готовности Кг системы можно осуществить двумя способами - путем составления дифференциальных уравнений на основании графа состояния системы и методом Половко.

Нахождение Кг методом дифференциальных уравнений

Для графа состояний рассматриваемой системы система дифференциальных уравнений имеет вид:

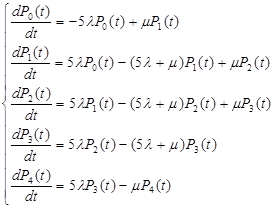
Нормировочное условие:

Начальные условия для системы дифференциальных уравнений:

P0(0)=1

P1(0)=0

P2(0)=0

P3(0)=0

P4(0)=0

Если предположить, что потоки стационарны, то есть и , = const, то можно получить следующую систему:

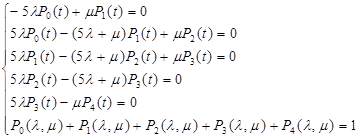
Тогда, исключая, например, четвертую строку как линейно зависимую от трех первых и пятой, можно получить следующую систему уравнений:

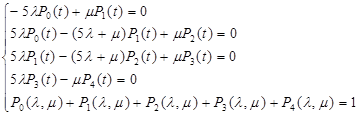
Система дифференциальных уравнений в матричном виде будет иметь вид:

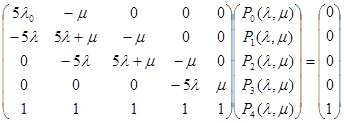
Отсюда имеем:

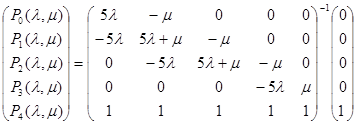
Решением системы будет:

Для заданных значений = 0.8 1/ч и m = 0.05 1/ч коэффициент готовности Кг принимает следующее значение:

Кг = P0 + P1 + P2 + P3 = 1 - Р4 = 0.02469

Нахождение Кг методом Половко

Кг = P0 + P1 + P2 + P3 = 1 - Р4 = 0.02469

Значения Кг, полученный методом Половко, совпадает с предыдущим расчетным, что подтверждает правильность его нахождения.

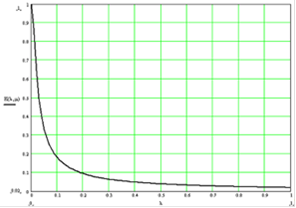
Зависимость коэффициента готовности системы Кг от интенсивности отказов основных элементов l приведена на графике:

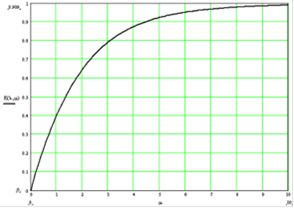
Зависимость коэффициента готовности системы Кг от интенсивности восстановления m приведена на графике:

Средняя наработка на отказ

Для заданных значений m = 0.05 1/ч и Кг = 0.02469 среднее время наработки на отказ принимает следующее значение:

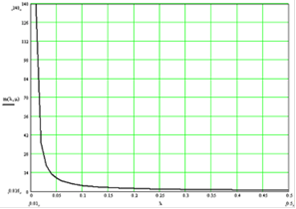
Зависимость среднего времени наработки на отказ от интенсивности отказов представлена на графике:

Зависимость времени наработки на отказ от интенсивности восстановления представлена на графике:

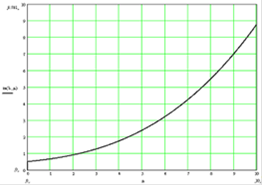
Среднее время восстановления системы

Перейти на страницу: 1 2 3

Другое по теме:

Техника антенных устройств Развитие антенной техники на всем протяжении эволюции радио сопровождалось и было тесно связано с развитием теории антенных устройств. Уже первая работа Генриха Герца по экспериментальному доказательству существования электромагнитных волн была им ...