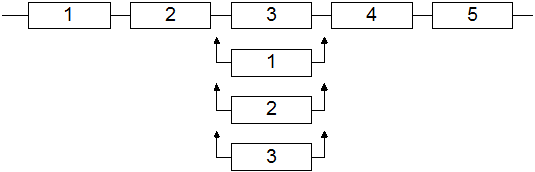
В качестве состояния системы выберем количество неисправных элементов. Будем считать, что в системе имеется только одно восстанавливающее устройство. Тогда граф состояний системы примет вид:
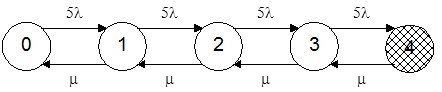
Рабочими для системы являются состояния с 0 по 3, состоянием отказа системы является состояние 4.
Расчет основных характеристик системы
Для определения вероятности безотказной работы системы составим систему дифференциальных уравнений, соответствующую графу состояний, запретив переход из отказового состояния 4 предотказовое состояние 3.
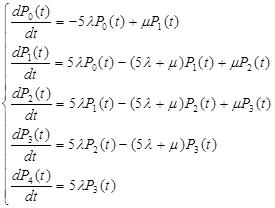
Нормировочное условие: 
Начальные условия для системы дифференциальных уравнений:
P0(0)=1
P1(0)=0
P2(0)=0
P3(0)=0
P4(0)=0
При расчете методом дифференциальных уравнений, после применения прямого преобразования Лапласа при начальных условиях система примет вид:
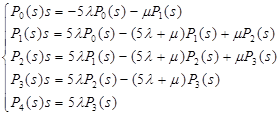
Система дифференциальных уравнений в матричном виде будет иметь вид:
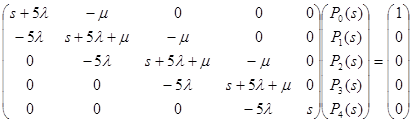
Отсюда имеем:
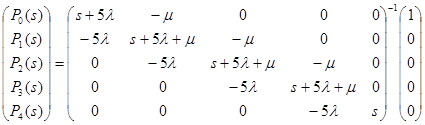
Таким образом:
Вероятность безотказной работы системы
Для определения вероятности безотказной работы необходимо применить к системе обратное преобразование Лапласа и подставить заданные значения для интенсивности отказов нагруженных элементов λ, интенсивности восстановления μ и времени работы t.
После обратного преобразования Лапласа система примет вид:
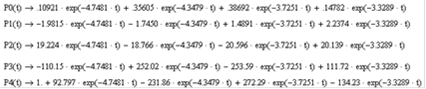
Функцию вероятности нахождения системы в рабочем состоянии, в силу наличия одного состояния отказа и нормировочного условия, можно записать следующим образом:
сист = P0(t)+P1(t)+P2(t)+P3(t)= 1-P4(t)
Для заданных значений t = 4 ч, l = 0.8 1/ч и μ = 0.05 1/ч Pсист = 14.53451·10-6.
Зависимость вероятности безотказной работы P(t) от времени работы системы представлена на графике:
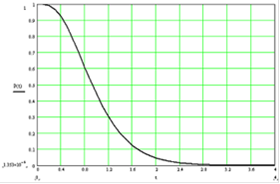
Из полученного графика видно, что с увеличением времени работы системы вероятность нахождения системы в рабочем состоянии падает.
Увеличение интенсивности отказов влечет за собой уменьшение вероятности безотказной работы системы.
Среднее время безотказной работы
Среднее время безотказной работы рассчитывается по формуле:
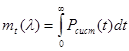
Для заданных значений t = 4 ч, 
= 0.8 1/ч и μ = 0.05 1/ч среднее время безотказной работы mt = 1.009 ч.
Зависимость среднего времени безотказной работы mt от интенсивности отказов элементов λ для μ = 0.05 приведена в таблице:
| λ | mt |
| 0.6 | 1.350 |
| 0.8 | 1.009 |
| 1.0 | 0.806 |
Зависимость среднего времени безотказной работы mt от интенсивности восстановления элементов μ для λ = 0.8 приведена в таблице:
| μ | mt |
| 0.0005 | 1.000 |
| 0.05 | 1.009 |
| 5 | 3.207 |
Другое по теме:
Параметры устройства, измеряющего толщину покрытия объекта и его метрологические характеристики Целью курсового проекта является изучение параметров устройства измеряющего толщину покрытия объекта и его метрологические характеристики. В результате намеченной работы мы должны из существующих методов по измерению толщины покрытия, выбрать на ...