При расчете y(nT) с помощью алгоритма ОБПФ исходной последовательностью является Y(jkw) - отсчеты выходного сигнала в частотной области.Y(jkw) найдем из соотношения:
![]()
Отсчеты X(jkw) иH(jkw) были определены выше. После вычислений имеем:(jkw) = {4,3124; 2,5222-j3,4214; -0,9033-j0,0325; 0,0791+j0,0321; 1,1524; 0,0791-j0,0321; -0,9033+j0,0325; 2,5222+j3,4215 }
Реализация алгоритма ОБПФ аналогична реализации алгоритма БПФ, за исключением различия весовых коэффициентов и того, что конечный результат необходимо разделить на N.
Для N = 4:= 1; W1 = j;
Для N = 8:= 1; W1 = 0,7071 + j 0,7071;= j; W3 = - 0,7071 + j 0,7071;
С помощью ОБПФ рассчитаемy(nT). Алгоритм и результаты поэтапного вычисления приведены на рисунке 6.
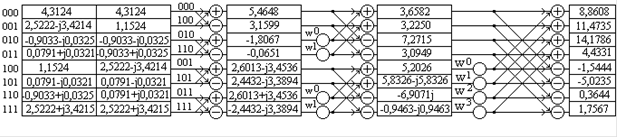
рис.6
После деления получившихся отсчетов на N = 8 имеем:(nT) = {1,1076; 1,434; 1,772; 0,554; -0,193; -0,628; 0,046; 0,22.}
Как известно существует три вида свертки дискретных сигналов:
a Линейная свертка, или же апериодическая
![]()
которая выполняется при небольшом количестве отсчетов x(nT) и h(nT) и применяется к непериодическим сигналам.
b Круговая свертка (периодическая),
![]()
которая применяется к периодическим сигналам. При выполнении круговой свертки необходимо, чтобы последовательности x(nT) и h(nT) имели одинаковый период повторения. Круговая свертка осуществляется на интервале равном одному периоду.) Секционированная свертка, с помощью которой осуществляется свертка сигналов большой длительности. Для этого сигнал разбивают на секции одинаковой длины. Способ обработки сигнала в каждой секции определяется импульсной характеристикой цепи h(nT). Каждая секция обрабатывается отдельно по формуле круговой свертки.
Так как входной сигал и импульсная характеристика, в нашем случае, имеют небольшое количество отсчетов, а входной сигнал - непериодический, то выходной сигнал y(nT) рассчитаем с помощью линейной свертки.
![]() = 0
= 0
![]() = 1
= 1
![]() = 2
= 2
![]() = 3
= 3
![]() = 4
= 4
![]() = 5
= 5
![]() = 6
= 6
![]() = 7
= 7
![]()
В результате выполнения линейной свертки имеем следующие значения выходной последовательности y(nT):(nT) = {0,8828; 1,4718; 1,7718; 0,5545; -0,1931; -0,6279; 0,0456; 0,2196}
Рассматривая результаты вычисления выходной последовательности y(nT), получившиеся после ОБПФ и линейной свертки, можно сказать, что при небольшом количестве отсчетов ОБПФ дает определенную погрешность. Следовательно в данном случае наиболее приемлемо, для вычисления выходной последовательности, использование линейной свертки.
Программа, для вычисления БПФ и ОБПФ приведена ниже.
CLX
LETpi = 3,141592654: m = 3
PRINT²Введите длину последовательности n²
20 INPUT n
PRINT ²²
DIM A(n): DIM B(n): DIM C(n): DIM D(n)
FOR i = 0 TO (n - 1)
PRINT ²a(²; i ;²) = ²: INPUT A(i)
PRINT ²b(²; i ;²) = ²: INPUT B(i)
60NEXTi
PRINT²²
PRINT²Введите 1, если БПФ или - 1, если ОБПФ²
90 INPUT u
LET k =1
LET C(k) = cos(- 2*pi*(k - 1)/n)
LET D(k) = sin(- 2*pi*(k - 1)/n)
IF k <=(n/2) THEN LET k = k+1: GOTO 100
LET i = 1
LET l = 1
LET r = 1
LET p = (r - 1)+(l - 1)*2i
LET q = p + 2(i - 1)
LET s = (r - 1)*2(m - i)
LET C(s) = C(s): LET D(s) = D(s)*u
LET A = A(p): LET B = B(p)
LET T1 = A(q)*C(s) - B(q)*D(s)
LET T2 = A(q)*C(s) + B(q)*D(s)
LET A(p) = A + T1: LET A(q) = A - T1 Перейти на страницу: 1 2
Другое по теме:
Разработка передающего полукомплекта ТУ С увеличением расстояния передачи, объёма информации и числа контролируемых объектов особое значение приобретает необходимость сокращения затрат на линии связи, обеспечения качества передачи сигналов и быстродействия системы передачи. Эти пробл ...