j – параметр потока, из первой задачи Nå_секj ;
j – среднее время задержки пакета в сети доступа, 
= 0,005 с.
Из формулы (2.17) следует зависимость максимальной величины для средней длительности обслуживания одного пакета от среднего времени задержки в сети доступа.
|
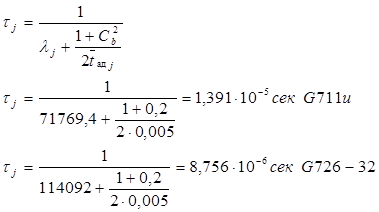
Построим данные зависимости при помощи прикладной программы MathCad.
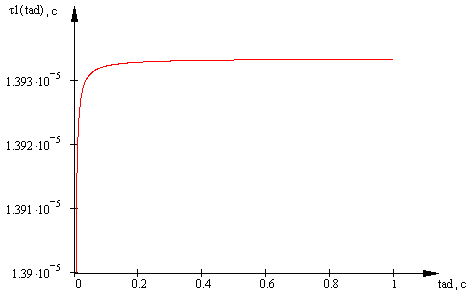
Рисунок 2 - Зависимость максимальной величины для средней длительности обслуживания одного пакета от среднего времени задержки в сети доступа для кодека
G
.711
u
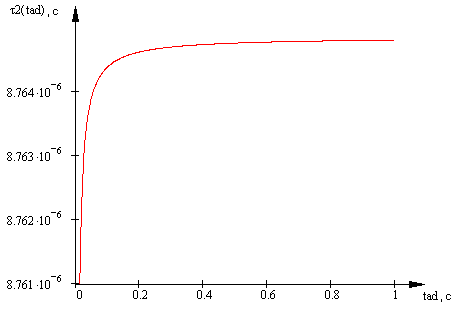
Рисунок 3 - Зависимость максимальной величины для средней длительности обслуживания одного пакета от среднего времени задержки в сети доступа для кодека
G
.726-32
Интенсивность обслуживания связана со средним временем задержки пакета в сети доступа обратно пропорционально:
|
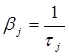
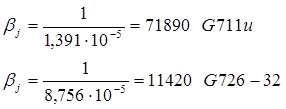
Время tj должно выбираться как минимальное из двух возможных значений. Первое значение – величина, полученная из последней формулы. Второе значение – та величина, которая определяется из условия ограничения загрузки системы – r. Обычно эта величина не должна превышать 0,5.
При среднем значении задержки в сети доступа 5 мс коэффициент использования равен:
|
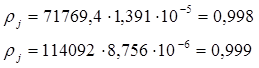
Рассчитать коэффициент использования для случаев с различными кодеками.
При таком высоком использовании малейшие флуктуации параметров могут привести к нестабильной работе системы. Определим параметры системы при её использовании на 50%. Средняя длительность обслуживания будет равна
|
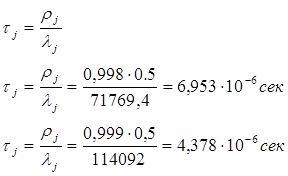Перейти на страницу: 1 2 3 4 5 6 7 Другое по теме:
Обеспечение надежности работы аппаратуры Понятие надежности. Один из основных параметров радиоэлектронной аппаратуры (РЭА) – надежность. Она зависит как от надежности используемой элементной базы, так и от принятых схемотехнических и конструкторских решений. Требования к надежнос ...