Алгоритмы функционирования вторичных преобразователей при измерении угловых и линейных перемещений могут иметь специфические особенности. Остановимся на двух частных случаях.
Кодовые датчики и сельсины при измерении угла в пределах одного оборота являются статическими, то есть при подаче на них питания они выдают значение углового положения в данный момент времени, независимо от того, были ли изменения положений при нахождении датчика в выключенном состоянии. Однако в статическом режиме невозможно зафиксировать полное угловое перемещение, если оно превышает целый оборот. Это перемещение можно зафиксировать только в динамическом режиме, фиксируя все переходы угла через нуль с учетом направления перехода, что определяет знак приращения в счетчике числа полных оборотов. При этом очевидно, что полные обороты, совершенные при выключенном датчике, не фиксируются.
Аналогичная ситуация наблюдается при вторичной обработке квадратурных сигналов датчиков с периодическими структурами (линейные или угловые индуктосины или растровые фотоэлектрические датчики). На рис.7, а показана зависимость этих сигналов от величины перемещения (на рисунке исключены постоянные составляющие, которые имеются в сигналах растровых датчиков, поскольку их величина не влияет на алгоритмы обработки). Шаг линеек равен ∆х. Амплитуды сигналов предполагаются равными. В противном случае они могут быть скорректированы при обработке.
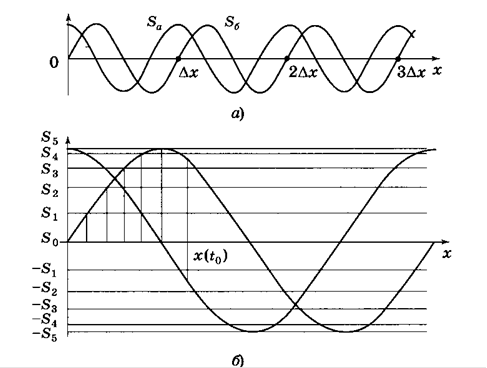
Рис. 7.
Непосредственно из рисунка видно, что величину полного перемещения можно найти, определив целое число шагов и часть шага, соответствующую моменту отсчета. Если перемещение происходит в одном направлении, число полушагов можно определить, подсчитывая переходы через нуль любого одного сигнала. Однако при этом нельзя определить даже направление перемещения. Изменение направления движения никак не будет фиксироваться. Поэтому, подсчитывая число переходов через нуль, можно определить полный путь, но не координату. Наличие двух сигналов устраняет эту проблему. При движении в положительном направлении последовательность переходов через нуль с учетом знака производной имеет вид +а, +б, - а, - б, +а,…., что соответствует приращению координаты при каждом переходе на четверть шага. При движении в обратном направлении последовательность переходов будет иной: +
а, - б, - а, +б, +
а,…., и каждый переход через нуль уменьшает координату на четверть шага. Если в процессе движения происходят реверсы, то каждый переход через нуль изменяет координату на четверть шага, а знак этого изменения определяется направлением перемещения. Признаком реверса является последовательное появление в одном из квадратурных сигналов двух одинаковых переходов через нуль. Таким образом, анализируя и соответствующим образом подсчитывая переходы квадратурных сигналов через нуль, можно определить координату с дискретностью в четверть шага линейки датчика.
Меньшую дискретность (имеется в виду малый шаг квантования) можно получить, используя значения сигналов в момент считывания координат. Алгоритм интерполяции можно пояснить следующим образом. Пусть периодические сигналы Sa (t) и S6 (t), сдвинутые относительно друг друга на четверть шага, имеют стабильную одинаковую форму, будучи четными функциями относительно осей, проходящих через экстремумы, и нечетными относительно осей, проходящих через нулевые значения сигналов. Отличие этих функций от моделей в виде синусоиды или кусочно-линейной функции не имеет принципиального значения, важна стабильность их формы. Разобьем четверть шага шкалы на п равных интервалов и обозначим через S - верхние границы этих интервалов (рис.2.7, б). Тогда, как видно из рисунка, абсолютное значение поправки σх при снятии отсчета перемещения в момент времени t0 можно рассчитать по формуле
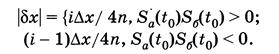(2.6) Перейти на страницу: 1 2 3
Другое по теме:
Разработка передающего полукомплекта ТУ С увеличением расстояния передачи, объёма информации и числа контролируемых объектов особое значение приобретает необходимость сокращения затрат на линии связи, обеспечения качества передачи сигналов и быстродействия системы передачи. Эти пробл ...