На последнем этапе синтеза осуществляется параметрическая оптимизация найденного схемного решения. Для этого составляют математические соотношения для всех 
. Продемонстрируем это на примере 
. Первые два слагаемых (табл. 8) вытекают непосредственно из выражения (63) (
определено на первом этапе синтеза). Два вторых слагаемых – это произведение коэффициента передачи масштабного усилителя-сум-матора на соответствующие поправочные коэффициенты. Последнее слагаемое, характеризующее влияние 
, было найдено на третьем этапе решения задачи.
Коэффициент передачи сумматора определяется следующим образом. За общую точку выберем инвертирующий вход ОУ2, тогда при идеальном ОУ1
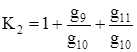. (67)
Аналогично, когда 
, 
,
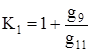. (68)
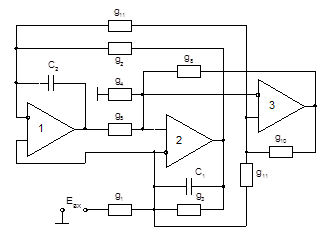
Рис. 12. Низкочувствительное ARC-звено на базе D элемента Антонио с собственной компенсацией
При параметрической оптимизации функция цели может быть различна и составляется из практических соображений. Если необходима компенсация изменений всех параметров с точностью до величины 
, то из 
, 
, 
исключаются слагаемые, пропорциональные 
, затем из соотношения (57) определяются 
, 
и находятся приведенные в последней строке табл. 8 условия компенсации.
Рассмотренный пример наглядно иллюстрирует методический аспект синтеза структурных схем на базе принципа собственной компенсации.
В рамках генетического подхода алгоритм синтеза структуры будет содержать следующие базовые составляющие.
Генерация схем с заданным набором функциональных свойств. Принципиально на этом этапе можно не учитывать частотные свойства активных элементов. Однако, как это следует из рассмотренного примера, чрезвычайно большое их влияние может в дальнейшем увеличить активную составляющую общей чувствительности.
Ранжирование набора схем по степени влияния параметров активных элементов и числу степеней свободы. Здесь предпочтение отдается схемам с большим числом неиспользованных (заземленных) входов активных элементов, поэтому последующее применение принципа собственной компенсации может заметно снизить влияние паразитных параметров активных элементов.
Функционально полный анализ схем с целью вычленения локальных передаточных функций и набора 
(k – номер дополнительного входа).
Выбор доминирующих по чувствительности активных элементов и образование по изложенной методике дополнительных компенсирующих контуров обратной связи.
Параметрическая оптимизация схемы с целью минимизации влияния активных элементов на основные параметры и характеристики.
Настоящий алгоритм воспроизводит метод усечения и положен в основу дальнейших исследований.
Рассмотрим применение предложенной методики к синтезу малошумящих D-элементов с расширенным частотным диапазоном, которые позволяют потенциально создавать «бездрейфовые» ограничители спектра Из анализа принципиальных схем устойчивых D-элементов (рис. 6–9) видно, что только в схемах Антонио дрейф нуля определяется входными токами неинвертирующих входов ОУ, которые легко минимизируются применением на входе «алмазных» транзисторов и их эквивалентов.
Так, в схеме Антонио с емкостной нагрузкой дополнительным входом схемы для организации компенсирующего контура обратной связи целесообразно использовать эту емкость. В этом случае дополнительные передаточные функции, будут иметь следующий вид: Перейти на страницу: 1 2 3 4 5 6 7
Другое по теме:
Совершенствование системы контроля длины заготовки установки для гибки прутков Интенсификация экономики на современном этапе обусловлена ускорением научно-технического прогресса, одно из основных направлений которого — автоматизация и механизация производства. Одно из основных направлений развития машиностроения - шир ...