Для звеньев второго порядка ФНЧ условие (4) можно исключить, тогда, как следует из (3), основные параметры будут иметь следующий вид
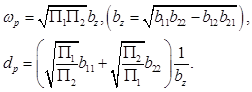(24)
Перебор вариантов реализации 
показывает, что 
, поэтому параметры передаточной функции (5) можно конкретизировать:
,
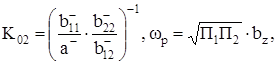
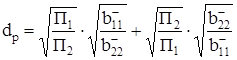. (25)
Таким образом, сдвиг частоты полюса в область более низких частот 
сопровождается увеличением коэффициента усиления звена K02. Однако в любом случае минимальное значение затухания полюса соответствует аналогичному параметру разделенной пассивной RC-цепи 
, что препятствует реализации ФНЧ со специальными свойствами (например, ФНЧ с линейной ФЧХ). Тогда при П1=П2, 
в диапазоне рабочих частот
(26)
. (27)
Таким образом, эффекта «перенапряжения» не наблюдается и верхняя граница динамического диапазона определяется соотношением (19), а собственный шум схемы – коэффициентом влияния (15)
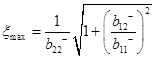(28)
и, следовательно, при большем К02 первым ОУ. Однако при небольших коэффициентах передачи «вклад» ОУ в собственный шум схемы практически одинаков.
Полученные соотношения показывают, что основной задачей этапа схемотехнического проектирования безъемкостных ФНЧ является создание структур, в рамках которых параметрическая оптимизация обеспечивает реализацию любых значений добротности при более низком влиянии ОУ на собственный шум звена второго порядка. Как было показано ранее, решение такой задачи возможно применением принципа собственной компенсации влияния, по крайней мере, одного из ОУ. Для уменьшения затухания полюса, вызванного влиянием площади усиления доминирующего ОУ, на его выходе должна быть реализована передаточная функция ФНЧ, а возвратное отношение дополнительной (компенсирующей) обратной связи должно быть положительно.
Принципиальная схема приведена на рис. 1.
Рис. 1. Звено R-фильтра с собственной компенсацией влияния ОУ2
Для наглядности и упрощения последующих соотношений будем использовать базовые параметры масштабных усилителей
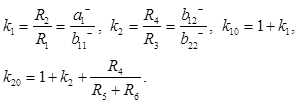(29)
В базисе указанных аргументов параметры передаточной функции Ф2(р) будут определять следующими соотношениями
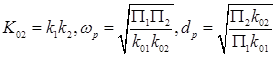(30)
при выполнении параметрического условия собственной компенсации
, при 
,
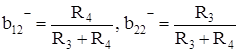, (31)
, где 
, 
.
Аналогично при тех же условиях определяются локальные передаточные функции
(32)
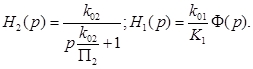(33)
Таким образом, как это следует из (19) и (20), максимальное выходное напряжение звена определится следующим выражением
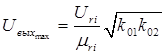(34)
при условии
.
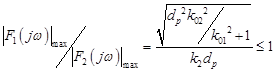(35)
Соотношение (35) является оценочным при 
.
При аналогичном допущении определяется коэффициент влияния ОУ1 и ОУ2 на собственный шум схемы
. (36)
Таким образом, введение компенсирующего контура обратной связи существенно уменьшило влияние ОУ2 на основные качественные показатели схемы звена второго порядка. Для построения и моделирования принципиальных схем разработан, ориентированный на SiGe технологию, SGB25VD (IHP) ОУ, базовые параметры которого показаны в табл. 2. Здесь и далее приводятся результаты моделирования принципиальных схем в среде Cadence. Перейти на страницу: 1 2 3
Другое по теме:
Каналы связи и интерфейсы Тема контрольной работы по дисциплине "Информационные измерительные системы" "Каналы связи и интерфейсы". Появление ИИС обусловлено в первую очередь конкретными задачами производства и научных исследований, требующих получе ...