Задание:
Используя метод гармонической линеаризации нелинейного элемента, определить на основе частотного способа возможность возникновения автоколебаний в замкнутой системе, их устойчивость, амплитуду и частоту.
Исходные данные:
Структура нелинейной САУ представлена на рис. 3.1, где НЭ— нелинейный элемент, W(s) - передаточная функция непрерывной линейной части системы.
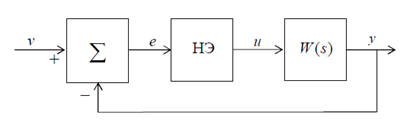
Рис 3.1
1. Передаточная функция W0(s) берется из пункта 1, как передаточная функция скорректированной системы с соответствующими числовыми коэффициентами. Нелинейный элемент НЭ имеет нелинейную характеристику u=f(e) которая для всех заданий является характеристикой идеального реле:
где с=2.
Приближенная передаточная функция нелинейного элемента для случая идеальное реле имеет вид:
где a – амплитуда искомого периодического режима, а>0.
2. На комплексной плоскости строим характеристику:
Это прямая, совпадающая с отрицательным отрезком действительной оси, вдоль которой идет оцифровка по амплитуде а0 = 0, a1, a2, …. В том же масштабе на комплексной плоскости строится АФЧХ разомкнутой системы W0(jw) при изменении частоты от 0 до + inf.
Передаточная функция скорректированной системы:
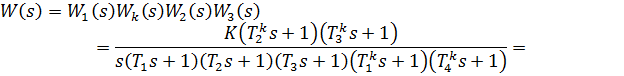
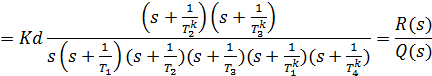
На рис.3.2 (выделен интересующий фрагмент) пунктиром отмечена АФЧХ
рис.3.2
Точка пересечения кривых (-0,165; -0j).
В точке пересечения АФЧХ W0(jw) и прямой 
по графику W(jw) находятся частота искомого периодического (гармонического) режима w=w*, а на прямой в точке пересечения его амплитуда а = а*. Тогда в системе существуют периодические колебания:
Приравнивая Im(W0(jw))=0 находим w*=1,065 (функция fsolve). При найденном значении частоты получим Re(W0(jw*))=-1,3. Из условия Re(W0(jw*))=
находим а*=0.41.
Для определения устойчивости периодического режима можно воспользоваться следующим правилом: если при увеличении амплитуды а вдоль кривой 
пересечение АФЧХ W0(jw) происходит «изнутри наружу», то такой периодический режим будет устойчивым, т.е. в системе существуют автоколебания с частотой w* и амплитудой а* .
Таким образом, периодический режим будет устойчивым.
Другое по теме:
Микроконтроллеры семейства AVR фирмы Atmel В классической микропроцессорной системе используются отдельная микросхема процессора, отдельные микросхемы памяти и отдельные порты ввода вывода. Стремительное развитие микропроцессорной техники требует всё большей и большей степени интеграции ...