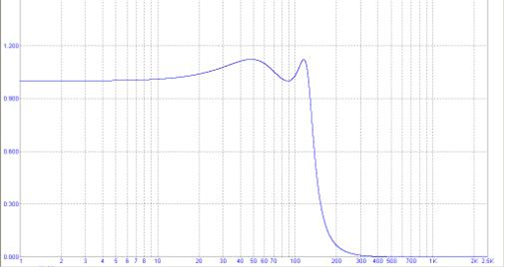
По передаточной функции построим модуль Н(f), который имеет вид:
Передаточная функция характеризует цепь в частотной области. Во временной области цепь характеризуется импульсной характеристикой h(nT).
Импульсная характеристика дискретной цепи представляет собой реакцию цепи на дискретную σ - функцию.
Импульсная характеристика и передаточная функция связаны между собой формулами Z-преобразования. Импульсную характеристику можно определить по известной передаточной функции, применяя теорему запаздывания к результатам деления полинома числителя на полином знаменателя.
Для того чтобы найти импульсную характеристику, для начала преобразуем передаточную функцию, получаем:
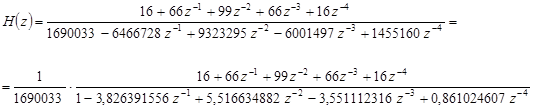
Разделим числитель передаточной функции на знаменатель:
H(z) = 
(16 + 127,2222649 z-1 + 497.536042 z-2 + 1324.746723 z-3 +
.279149 z-4 +
+ 4979.904763 z-5 + 8004.24748 z-6 + 11880.41043 z-7) = 0.000009467 +
.00007528z-1 +
+ 0.0002944z-2 + 0.0007839z-3 + 0.001644z-4 + 0.002947z-5 + 0.004736z-6 +
.00703z-7
Получили импульсную характеристику данного фильтра:
Расчеты деления приведены ниже:
Каноническая схема фильтра:
Канонической называют структурную схему фильтра, содержащую минимальное число элементов задержки.
Преобразуем передаточную функцию, получаем:
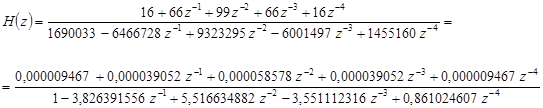
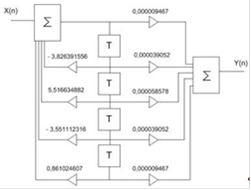
Другое по теме:
Расчет управляемого выпрямителя и СИФУ В настоящее системы преобразования переменного синусоидального напряжения и тока в постоянные практически полностью представлены полупроводниковыми выпрямителями. Очень часто также необходимо регулировать величину полученного постоянного напряже ...