Составляющая неустойчивости (SESR) на i-ом пролете ЦРРЛ за наихудший месяц в состоянии готовности ЦРРЛ рассчитывается
, % (14)
Коэффициент неготовности в условиях замираний на i-ом пролете ЦРРЛ за наихудший месяц определяется:
, % (15)
Так как на территории РФ явление субрефракции бывает только в летние месяцы (в степных районах), то часто можно считать, что 
=0 , 
=1 , 
=0 и расчет упрощается
, % (14)
, % (15)
где 
– процент времени, в течении которого величина коэффициента ошибок на выходе ЦРРЛ больше допустимой величины из-за интерференционных замираний на пролете;
– коэффициент готовности в условиях интерференционных замираний;
– коэффициент неготовности в условиях интерференционных замираний;
– процент времени, в течение которого величина коэффициента ошибок на выходе ЦРРЛ больше допустимой величины из-за гидрометеоров.
Для определения общей неустойчивости из-за интерференционных замираний необходимо рассчитать неустойчивость из-за «плоских» (
) и селективных (
) замираний. Соответственно:
(16)
(17)
Эффективное минимальное допустимое значение множителя ослабления 
рассчитываем по формуле:
(18)
где 
- запас на «селективные замирания
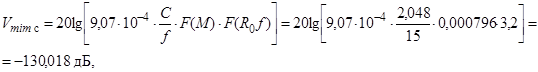
– пропускная способность ЦРРЛ, Мбит/с (см таблица 1);
– рабочая частота;
=3,2 – функция, зависящая от длины пролета и рабочей частоты /4,стр. 39, рис.4/;
- функция, зависящая от числа уровней и вида модуляции СВЧ сигнала. Согласно Таблице 1 имеем:
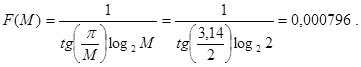(19)
Согласно вышеизложенным расчетам, общая неустойчивость из-за интерференционных замираний равна сумме:
% (20)
Интенсивность дождя
)
Тогда составляющая неустойчивости
Определение коэффициента неготовности в условиях интерференционных замираний 
на пролетах ЦРРЛ за наихудший месяц осуществляют по зависимости от медианного значения длительности замираний 
и от стандартного отклонения распределения длительности замираний 
Усредненное значение величины =4,855 дБ определяем согласно Перейти на страницу: 1 2
Другое по теме:
Расчет зеркальной параболической антенны с облучателем в виде конического рупора Параболические антенны в последнее время находят все более широкое применение в космических и радиорелейных линиях связи. В 1888 году известный немецкий физик Г. Герц в своих опытах по СВЧ оптике впервые применил в качестве фокусирующего устройс ...