Рассмотрим уравнения динамики ИМ. В схеме на рисунке 3.9 система координат 0ХУZ жестко связана корпусом датчика. ИМ по отношению к корпусу обладает двумя поступательными степенями свободы, перемещения по которым обозначим как х и у. Поступательные перемещения ограничены упругими связями с коэффициентами упругих сил cx и cy. Магнитоэлектрические ДС, создавая силу Ампера Fа обеспечивают возбуждение гироскопа, то есть сообщают ИМ плоские колебания вдоль оси ОХ с относительной скоростью 
. Основной реакцией гироскопа на вращение корпуса вокруг оси 0Z является образование вдоль оси ОY кориолисовых сил инерции FК, за счет взаимодействия скоростей ωz и , которые вызывают плоские колебания ИМ вдоль оси 0Y, являющиеся мерой угловой скорости ωz. Однако в общем случае будем считать основание вращающимся и с абсолютными угловыми скоростями ωх, ωу и поступательно перемещающимся с абсолютными линейными скоростями Vx , Vy , Vz . Кроме того, будем считать, что конструкция упругого подвеса ИМ обеспечивает только поступательные его перемещения в направлениях осей ОХ и ОУ.
Для составления уравнений динамики ДУС воспользуемся уравнениями Лагранжа второго рода :
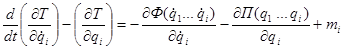,(4.1)
где 
- обобщенные координаты системы, соответствующие 
степеням ее свободы; 
- кинетическая энергия системы, выраженная через обобщение координаты и обобщенные скорости 
; 
- диссипативная функция, определяющая рассеивание энергии системы при ее движении; 
- потенциальная энергия системы; 
- прочие внешние силы (моменты) явным образом не зависящие от обобщенных координат и скоростей.
Для рассматриваемого ММГ 
. В общем случае силы 
могут учитывать и другие внешние возмущающие и управляющие воздействия. Введём систему координат 01ХмУмZм, связанную с ИМ, тогда
, (4.2)
, 
,
где 
и 
- векторы абсолютных линейных скоростей ИМ и несущей рамы;
- вектор абсолютной угловой скорости вращения несущей рамы;
- вектор относительного поступательного перемещения ИМ;
- орты системы координат ОХУZ.
Принимая во внимание, что
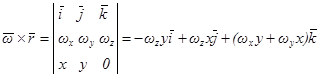
из уравнений (4.2) находим:
,
(4.3)
Пусть оси системы координат ОХмУмZм являются осями симметрии ИМ, не учитывая оптическую щель. Тогда его кинетическая энергия определится выражением:
,(4.4)
где m - ИМ.
Принимая во внимание основные конструктивные факторы гироскопа, запишем следующие выражения для его потенциальной энергии и диссипативной функции:
,
,(4.5)
где 
- коэффициенты сил вязкого трения, определяющие рассеивание энергии колебаний чувствительного элемента по координатам 
и 
.
Подставляя выражения (4.4) и (4.5) в уравнения (4.1) для обобщенных координат и , после вычислений находим уравнения движения ИМ: Перейти на страницу: 1 2
Другое по теме:
Каналы связи и интерфейсы Тема контрольной работы по дисциплине "Информационные измерительные системы" "Каналы связи и интерфейсы". Появление ИИС обусловлено в первую очередь конкретными задачами производства и научных исследований, требующих получе ...