(4.23)
(4.24)
Используя уравнение (4.24), мы можем получить циклическую частоту гармонической функции линеаризации, она будет равна
(4.25)
Подставив уравнение (4.23) в (4.21), получим уравнение восьмого порядка
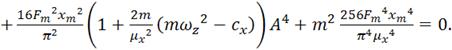
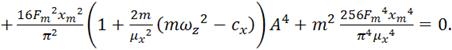(4.26)
Добавим новые переменные
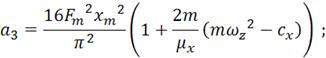
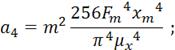
(4.27)
тогда
(4.28)
для решения этого уравнения четвёртого порядка найдём решение следующего уравнения третьего порядка
(4.29)
Добавим новые переменные
(4.30)
тогда
(4.31)
Действительный корень этого уравнения
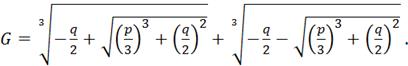
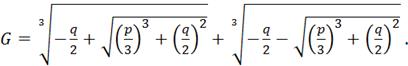(4.32)
Четыре корня уравнения (4.28) могут быть найдены, как
;
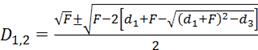
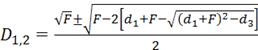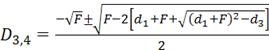
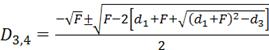(4.33)
Амплитуда гармонической функции линеаризации равна
;
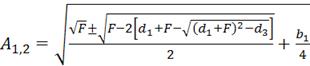
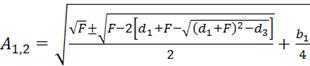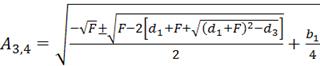
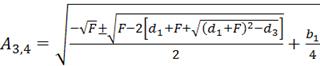. (4.34)
Последовательно решив уравнения (4.32) и (4.30), найдём корни D1,2,3,4 по уравнениям (4.33). Отбросив мнимые значения корней D3,4, и приводящий к нереальным значениям амплитуды корень D2, получаем
.
Тогда, в соответствии с уравнениями (4.35),
м.
Теперь, используя уравнение (4.25), получим
Гц.
Сравния данное аналитическое решение с результатами моделирования, полученными в пункте 4.3 (
), видим, что они достоверны. А значит данный аналитический метод решения может быть использован для анализа характеристик автоколебательного ММГ. Перейти на страницу: 1 2
Другое по теме:
Импульсный блок питания на базе БП ПК Тема «Импульсный блок питания на базе БП ПК» Предлагаемое устройство помимо неплохих технических характеристик, привлекательно тем, что за его основу взят импульсный блок питания отслужившего свой срок IBM-совместимого персонального компьютера ...