Множество R называется линейным пространством, если
1) в R определена операция "сложения", которая подчиняется всем правилам сложения: если f Î R, g Î R, то f + g Î R; в R имеется нулевой элемент 0 такой, что 0 +f = f для всех f Î R;
2) в R определена операция умножения элемента f Î R на числа a из множества К (a Î К, f Î R Þ a f Î R). Чаще всего К – множество всех действительных или комплексных чисел.
В дальнейшем будем рассматривать только линейные пространства.
Рассмотрим отображение Т, которое каждому элементу f Î R однозначно ставит в соответствие элемент h Î R*, где R* является также линейным пространством. Если R* = R, то Т отображает R в самого себя. Отображение Т называется оператором и отображение R в R* записывается в виде уравнения
T f = h (f Î R, h Î R*).
В частном случае, когда R* - пространство комплексных чисел, Т носит название функционала.
Пусть уравнение
T f = h
имеет единственное решение и каждому элементу h Î R* можно поставить в соответствие единственный элемент f Î R. Оператор, осуществляющий это соответствие, называется обратным по отношению к Т и обозначается Т-1. Таким образом можно записать
f = T-1 h.
Пример. Пусть имеется система линейных уравнений
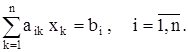
Представим эту систему в матричном виде

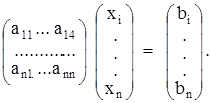
Если ввести пространство матриц – столбцов R, то ![]() где
где
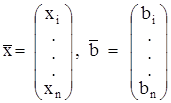
и ![]() Здесь оператор А – матрица размера n x n
Здесь оператор А – матрица размера n x n
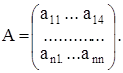
Если матрица А невырождена, то обратная матрица и является обратным оператором:
![]()
Определение. Линейное пространство R называется метрическим, если каждой паре элементов х, y Î R ставится в соответствие вещественное число r (x, y) – расстояние между x и y – удовлетворяющее условиям:
1. r (x, y) ³ 0, если r (x, y) = 0, то x = y;
2. r (x, y) = r (y, x);
3. r (x, y) £ r (x, z) + r (z, y) (неравенство треугольника).
Если введением расстояния пространство R превращено в метрическое пространство, то говорят, что в пространстве R введена метрика.
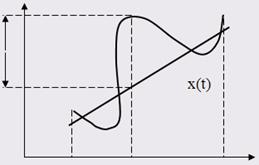
В радиотехнике элементами пространства являются сигналы (токи или напряжения), математическими моделями которых являются функции времени x(t), y(t), . . Рассмотрим следующее пространство сигналов.
1. С - пространство непрерывных на промежутке функций с метрикой:
![]()
![]() y(t)
y(t)
r(x,y)
2. L2(a, b) - пространство интегрируемых в квадрате функций (x(t) Î L2(a, b), если ![]() с метрикой
с метрикой
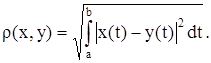
Определение. Элементы линейного пространства R называются линейно независимыми, если из условия Перейти на страницу: 1 2
Другое по теме:
Исследование RC–автогенераторов для операционных усилителей с мостом Вина Генератором гармонических колебаний называют устройство, которое без постоянного возбуждения преобразует энергию источника питания в энергию гармонических колебаний. Операционный усилитель – это аналоговая интегральная схема, снабженная, как ...