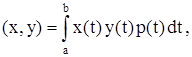
где р(t) – некоторая положительная, непрерывная на интервале функция. Для отрезка и p(t) = 1 получаем полиномы Лежандра; для отрезка и 
- полиномы Чебышева первого рода; для полупрямой и p(t) = е-t – полином Лягерра; для всей оси (-¥, ¥) и p(t) = е-t – полином Эрмита и т.д.
Определение. Линейное метрическое пространство R называется полным, если оно содержит все предельные точки. Это значит, если r(хm+p, xn) ® 0 при m ® ¥ (xm Î R), " p = 
, то $ хо Î R такое, что lim r(xm, xo) = 0.
m ®¥
Определение. Полное метрическое пространство называется пространством Банаха.
Полное унитарное пространство носит название пространства Гильберта.
Примеры.
1. Пространство L(a, b) – абсолютно интегрируемых на интервале (а, b) функций (x(t) Î L(a, b), если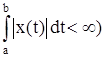 
с метрикой
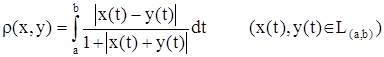
является пространством Банаха.
3. Пространство L2 (a, b), со скалярным произведением
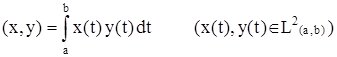
является пространством Гильберта. Перейти на страницу: 1 2
Другое по теме:
Разработка конструкции, топологии и технологического процесса изготовления интегральной микросхемы усиления тока индикации кассового аппарата Основополагающая идея микроэлектроники – конструктивная интеграция элементов схемы – приводит к интеграции конструкторских и технологических решений, при этом главной является задача обеспечения высокой надежности ИМС. Важнейшей задачей п ...