Определение. Линейное нормированное пространство R называется унитарным, если в нем введено скалярное произведение, которое каждой паре элементов x, y Î R ставит в соответствие действительное или комплексное число (x, y), удовлетворяющее условиям
1. (x, y) = (y, x)* ( * - знак комплексного сопряжения);
2. (a1 х1 + a2 х2, y) = a1(x1, y) + a2(x2, y) (a1, a2 Î K);
3. (x, x) ³ 0, если (х, х) = 0, то х = 0.
В унитарном пространстве норма вводится следующим образом
Теорема 1. Для " х, y унитарного пространства R справедливо неравенство Шварца
Равенство имеет место лишь для линейно зависимых элементов.
Теорема 2. Для " х, y унитарного пространства R имеет место неравенство
Равенство имеет место, если один из элементов х или y равен нулю или, когда х = l y (l > 0).
Теорема 3. Для " х, y унитарного пространства R выполняется равенство параллелограмма
Равенство имеет место, если один из элементов х или y равен нулю или, когда х = l y (l > 0).
Определение. Два элемента х, y Î R (x ¹ 0, y ¹ 0) называются ортогональными, если (х, y) = 0.
Система элементов e1, e2, . . . , en, . . . унитарного пространства R называется ортонормированной, если
Пусть система элементов х1, х2, . . . , хn, . . . ортогональна ((xi, xj)=0, i ¹ j), тогда ее можно нормировать, положив
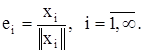
Из ортонормированности системы следует ее линейная независимость. Обратно – любую линейно независимую систему можно ортонормировать. Процесс ортонормированности следующий. Если система элементов y1, y2, . . . , yn, . . . –линейно независимая, то система e1, e2, . . . , en, . . ., где
становится ортонормированной.
Пусть теперь f – любой элемент унитарного пространства R, a e1, e2, ., en, . – ортонормированная система этого пространства. Величина
носит название коэффициента Фурье, а ряд
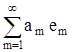
носит название ряда Фурье. Ряд Фурье наилучшим образом аппроксимирует f (приближается к f). Это значит, если рассматривать норму разности элемента f и ряда Фурье
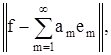
то наименьшее значение норма примет при
Можно показать, что выполняется неравенство
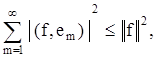
которое называется неравенством Бесселя.
Примеры ортонормированных систем:
1. Система гармонических функций, записанных в комплексном виде
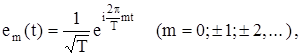
образуют ортонормированную систему в 
2. Функции
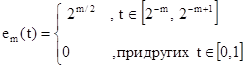
образуют для m = 1, 2, 3, .ортонормированную систему, состоящую из неотрицательных функций на отрезке
3. Ортонормированная система функций Уолша wal(m, x) 
заданная на интервале 
широко используется при дискретной обработке сигналов. Аналитическое описание функций Уолша довольно сложно. Легко понять принцип построения этих функций из графиков
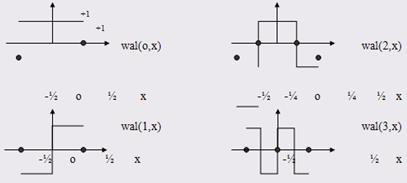
4. Важный класс ортонормированных систем можно получить при помощи ортогонализации функций 1, t, t2, ., tn, . в унитарном пространстве 
со скалярным произведением Перейти на страницу: 1 2
Другое по теме:
Расчет зеркальной параболической антенны с облучателем в виде конического рупора Параболические антенны в последнее время находят все более широкое применение в космических и радиорелейных линиях связи. В 1888 году известный немецкий физик Г. Герц в своих опытах по СВЧ оптике впервые применил в качестве фокусирующего устройс ...