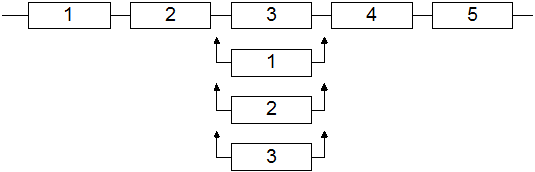
В качестве состояния системы выберем количество неисправных элементов. Будем считать, что в системе имеется только одно восстанавливающее устройство. Тогда граф состояний системы примет вид:
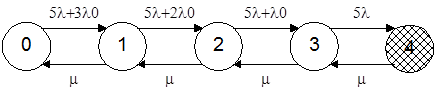
Рабочими для системы являются состояния с 0 по 3, состоянием отказа системы является состояние 4.
Для определения вероятности безотказной работы системы составим систему дифференциальных уравнений, соответствующую графу состояний, запретив переход из отказового состояния 4 предотказовое состояние 3.
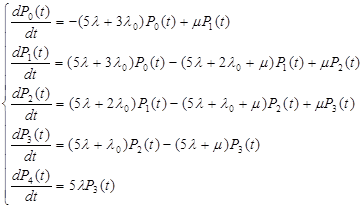
Нормировочное условие: 
Начальные условия для системы дифференциальных уравнений:
P0(0)=1
P1(0)=0
P2(0)=0
P3(0)=0
P4(0)=0
При расчете методом дифференциальных уравнений, после применения прямого преобразования Лапласа при начальных условиях система примет вид:
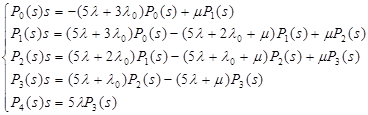
Система дифференциальных уравнений в матричном виде будет иметь вид:
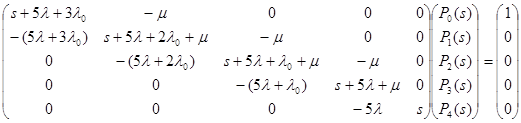
Отсюда имеем:
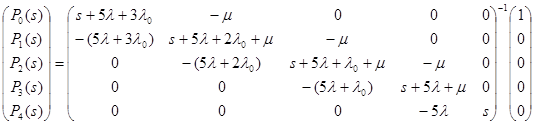
Таким образом:
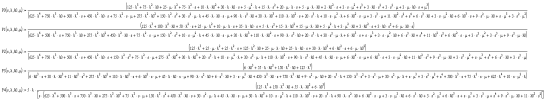
Вероятность безотказной работы системы
Для определения вероятности безотказной работы необходимо применить к системе обратное преобразование Лапласа и подставить заданные значения для интенсивности отказов нагруженных элементов λ, интенсивности отказов резервных элементов λ0, интенсивности восстановления μ и времени работы t.
После обратного преобразования Лапласа система примет вид:
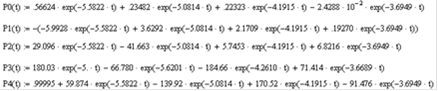
Функцию вероятности нахождения системы в рабочем состоянии, в силу наличия одного состояния отказа и нормировочного условия, можно записать следующим образом:
сист = P0(t)+P1(t)+P2(t)+P3(t)= 1-P4(t)
Для заданных значений t = 4 ч, l = 0.8 1/ч, l0 = 0.4 1/ч и μ = 0.05 1/ч Pсист = 0.26429·10-6.
Зависимость вероятности безотказной работы P(t) от времени работы системы представлена на графике:
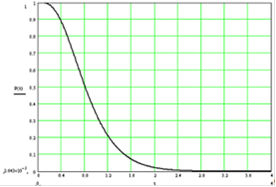
Из полученного графика видно, что с увеличением времени работы системы вероятность нахождения системы в рабочем состоянии падает.
Увеличение интенсивности отказов влечет за собой уменьшение вероятности безотказной работы системы.
Увеличение интенсивности отказов влечет за собой уменьшение вероятности безотказной работы системы.
Зависимость вероятности безотказной работы P(t) от времени работы системы t для различных значений интенсивности восстановления элементов μ представлена на графиках:
Среднее время безотказной работы
Среднее время безотказной работы рассчитывается по формуле:
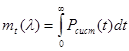
Для заданных значений t = 4 ч, 
= 0.8 1/ч, l0 = 0.4 1/ч и μ = 0.05 1/ч среднее время безотказной работы mt = 0.885 ч. Перейти на страницу: 1 2 3 4
Другое по теме:
Абстрактные цифровые автоматы Тема контрольной работы по дисциплине "Прикладная теория цифровых автоматов" - "Абстрактные цифровые автоматы". Цель работы - ознакомится с основными понятиями абстрактных цифровых автоматов; типами абстрактных автоматов; с ...