Зависимость среднего времени безотказной работы mt от интенсивности отказов нагруженных элементов λ для λ0 = 0.4, μ = 0.05 приведена в таблице:
| λ | mt |
| 0.6 | 1.141 |
| 0.8 | 0.885 |
| 1.0 | 0.724 |
Зависимость среднего времени безотказной работы mt от интенсивности отказов резервных элементов λ0 для λ = 0.8, μ = 0.05 приведена в таблице:
| λ0 | mt |
| 0.2 | 0.941 |
| 0.4 | 0.885 |
| 0.6 | 0.839 |
Зависимость среднего времени безотказной работы mt от интенсивности восстановления элементов μ для λ = 0.8, λ = 0.4 приведена в таблице:
| μ | mt |
| 0.0005 | 0.878 |
| 0.05 | 0.885 |
| 5 | 2.407 |
Коэффициент готовности
Нахождение коэффициента готовности Кг системы можно осуществить двумя способами - путем составления дифференциальных уравнений на основании графа состояния системы и методом Половко.
Нахождение Кг методом дифференциальных уравнений
Для графа состояний рассматриваемой системы система дифференциальных уравнений имеет вид:
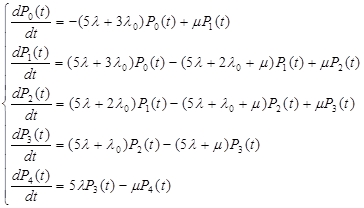
Нормировочное условие: ![]()
Начальные условия для системы дифференциальных уравнений:
P0(0)=1
P1(0)=0
P2(0)=0
P3(0)=0
P4(0)=0
Если предположить, что потоки стационарны, то есть ![]() и
и ![]() ,
,![]() = const, то можно получить следующую систему:
= const, то можно получить следующую систему:
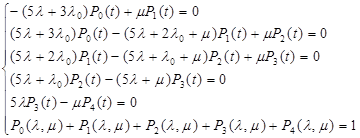
Тогда, исключая, например, четвертую строку как линейно зависимую от трех первых и пятой, можно получить следующую систему уравнений:
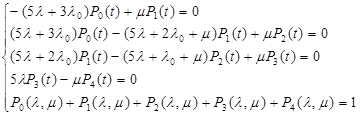
Система дифференциальных уравнений в матричном виде будет иметь вид:
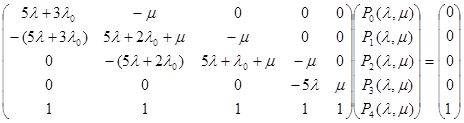
Отсюда имеем:
Другое по теме:
Синтез следящей системы с обратной связью по току и по скорости Состояние любого технического устройства характеризуется одной или несколькими физическими величинами. Совокупность предписаний, определяющих характер изменения выходных величин объектов, называется алгоритмом функционирования. К основным ...
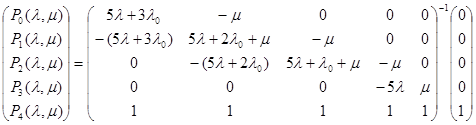 Перейти на страницу:
Перейти на страницу: