Технология цифровой связи

Можно показать, что для любого автомата Мили существует эквивалентный ему автомат Мура и, обратно, для любого автомата Мура существует эквивалентный ему автомат Мили.

При описании алгоритмов взаимной трансформации автоматов Мили и Мура в соответствии с изложенным выше мы будем пренебрегать в автоматах Мура выходным сигналом, связанным с начальным состоянием ( (a1)).

Рассмотрим сначала преобразование автомата Мура в автомат Мили.

Пусть дан автомат Мура: SA={ ХA, АA, УA,A,A, аоA}, где:

ХA={х1, х2,. хn}; Y={y1, у2,. уm}; А={ а0, а1, а2,. аN}; а0A = а0 - начальное состояние (а0AА); A - функция переходов автомата, задающая отображение (ХAхАA) - >АA; A - функция выходов автомата, задающая отображение АA->УA.

Построим автомат Мили: SB={ ХB, АB, YB,B, B, а0B}, у которого АB=АA; ХB=ХA; YB=УA; B=A; а0B=а0A. Функцию выходов B определим следующим образом. Если в автомате Мура A (аm, х1) = аs и A (аs) =yg, то в автомате Мили B (am, х1) =yg

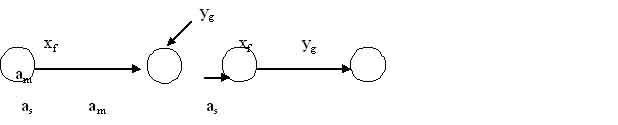
Рисунок 1.7 - Иллюстрация перехода от модели Мура к модели Мили

Переход от автомата Мура к автомату Мили при графическом способе задания иллюстрируется рис.1-7: выходной сигнал yg записанный рядом с вершиной (as), переносится на все дуги, входящие в эту вершину.

При табличном способе задания автомата таблица переходов автомата Мили совпадает с таблицей переходов исходного автомата Мура, а таблица выходов получается из таблицы переходов заменой символа as, стоящего на пересечении строки хf и столбца аm, символом выходного сигнала yg отмечающего столбец as в таблице переходов автомата SA.

Из самого способа построения автомата Мили SB очевидно, что он эквивалентен автомату Мура SA. По индукции нетрудно показать, что любое входное слово конечной длины, поданное на входы автоматов SA и SB, установленных в состояния am, вызовет появление одинаковых выходных слов и, следовательно, автоматы SA и SB эквивалентны.

Прежде чем рассмотреть трансформацию автомата Мили в автомат Мура, наложим на автомат Мили следующее ограничение: у автомата не должно быть преходящих состояний. Под преходящим будем понимать состояние, в которое при представлении автомата в виде графа не входит ни одна дуга, но которое имеет по крайней мере одну выходящую дугу. Итак, пусть задан автомат Мили:

SA={ ХA, АA,YA, A, A, a0A},

где:

ХA={x1, x2,. xn}; Y={y1, у2,. ym}; А={ a0,a1,a2,. aN}; a0A = a0 - начальное состояние (а0AА); A - функция переходов автомата, задающая отображение (ХAxАA) - >АA; A - функция выходов автомата, задающая отображение (ХAxАA) - >YA.

Построим автомат Мура: SB={XB, AB, YB, B, B, a0B}, у которого XB=XA; YB=YA.

Для определения AB каждому состоянию asАA поставим в соответствие множество As всевозможных пар вида (as, yg)

Функцию выходов B определим следующим образом. Каждому состоянию автомата Мура SB, представляющему собой пару вида (as,yg), поставим в соответствие выходной сигнал yg. Перейти на страницу: 1 2 3

Другое по теме:

Разработка автономного радиомаяка Актуальной проблемой на сегодняшний день является разработка новых методов получения электрической энергии, необходимой для питания электрооборудования автономных устройств, к которым относятся навигационные буи, речные бакены и т. п. В них исто ...