Тогда формулу (1) можно преобразовать
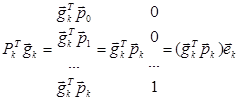
ек – (к+1) столбец единичной матрицы
С учетом всего этого формула (1) примет вид
Последнее выражение можно упростить, если матрица 
будет ортогональной. Ето возможно сделать, если вектора 
выбирать специальным образом. Вектора должны быть сопряженными относительно матрицы G, то есть должны выполняться следующие соотношения
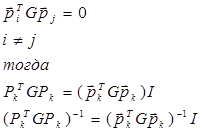
Тогда получаем упрощенное выражение
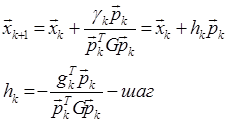
Таким образом мы установили, что среди методов минимизации квадратичных функций, укладывающихся в общую модельную схему, существует метод, к-тая итерация которого приводит в точку минимума функции Ф(
) на многообразии 
+
Рк-1.
Теоретически такой метод конечен, то есть он обеспечивает нахождение минимума функции Ф() не более чем за N шагов (N-размерность задачи), так как многообразие +Рк-1 на последнем N-том шаге совпадает с множеством значений аргумента и следовательно, если минимум функции Ф() не был найден ранее, то он обязательно будет найден на этом шаге.
Для того, чтобы полностью определить метод сопряженных градиентов необходимо определить правило выбора вектора 
. Это правило выглядит следующим образом:
(2)
- скаляр, который выбирается по двум теоретически эквивалентным формулам:
1. 
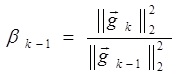- формула Флетчера-Ривса
2. 
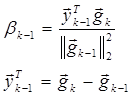- формула Полака-Рибьера
Метод сопряженных градиентов для квадратических функций легко обобщается на случай целевой функции общего вида. Для этого необходимо ввести процедуру одномерного поиска длины шага hk и определиться, всегда ли направление поиска будет выдаваться по формуле (2) или допустимы отступления от нее. Такие отступления называются восстановлениями или рестартами. В начале рестарта вектор 
. Метод сопряженных градиентов, использующий такие рестарты, называется традиционным. Традиционный метод сопряженных градиентов сходится в тех же предположениях, что и метод наискорейшего спуска. Он обладает теоретической N-шаговой сверхлинейной сходимостью, но из-за наличия ошибок округления реальная скорость сходимости метода сопряженных градиентов практически всегда линейна.
Таким образом, хотя схема метода сопряженных градиентов далека от идеала, тем не менее этот метод остается единственным разумным средством для решения задачи оптимизации очень большой размерности (число переменных более 1000000). Перейти на страницу: 1 2 3 4
Другое по теме:
Наблюдатель Люенбергера На практике достаточно распространенной является ситуация, когда не все компоненты вектора состояний доступны для измерения. В этом случае, чтобы в системе управления возможно было использовать обратную связь по состоянию, необходим ...