В данной курсовой работе в качестве метода синтеза применяется метод сопряженных градиентов. В группе данных методов процедура вычисления направления поиска не предполагает решения каких либо СЛАУ. Эти методы принципиально отличаются от методов Ньютна и квазиньютоновских методов.
Рассмотрим задачу поиска минимума квадратичной функции вида:
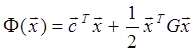
с,G - вектор и полноопределенная матрица, независящие от вектора 
.
Предполагается, что нам известно к-тое приближение в точке минимума
и (к+1) линейно независимых векторов 
.
Будем искать точку минимума целевой функции Ф() на линейном множестве векторов +
Рк, где Рк – (к+1)-мерное множество, образованное линейно независимыми векторами.
Множества, образованные вида 
+Рк называются линейными многообразиями.
Задача сводится к нахождению точки минимума Ф() на этом линейном многообразии.
Для решения этой задачи сначала вводится матрица Рк=> Введение такой матрицы позволяет сформулировать задачу поиска минимума функции Ф() на многообразии +Рк следующим образом: найти 
То есть надо найти вектор 
, таким образом, чтобы точка 
была бы точкой минимума функции 
.
Для решения этой задачи необходимо сначала в функцию Ф(х) вместо , затем продифференцировать получившуюся функцию по вектору , приравнять результат к нулю и оттуда выразить вектор
, который является решением задачи.
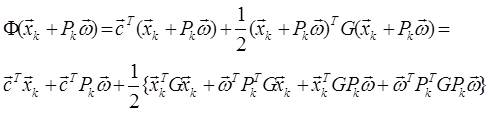
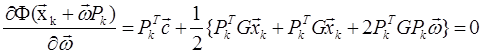
Если есть функция
, то 
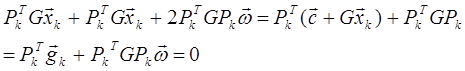
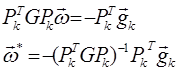
Тогда точка минимума
(1)
Формулу (1) можно рассматривать как формулу рекуррентного расчета точки в классических методах спуска. Другими словами, формула (1) описывает процедуру пошаговой минимизации квадратичной функции Ф(х).
Формула (1) обладает рядом свойств:
,
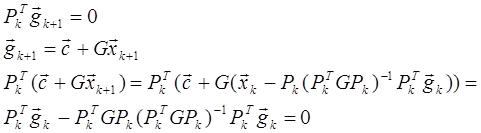
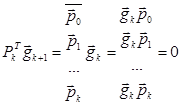то есть каждая компонента должна быть равна нулю
Так как предполагается, что все точки xj при j=1,к рассчитывается по формуле (1), то справедливо следующее свойство:
i>j Перейти на страницу: 1 2 3 4
Другое по теме:
Разработка технологии сборки и монтажа ячейки трехкоординатного цифрового преобразователя перемещения Рассматриваемая ячейка входит в трёх-координатного цифрового преобразователя перемещений. Преобразователь должен обеспечивать преобразование угловых координат со следующими точностными и динамическими характеристиками: - ...