![]()
![]()
Передаточная функция по ошибке при f= 0, которая позволяет выразить ошибку e(t) в системе при известном входном воздействии:
![]()
Передаточная функция по возмущению при и = 0 позволяет выразить влияние возмущения на выходной сигнал:
![]()
2.
. Передаточная функция разомкнутой исходной системы имеет вид W(s) = K/sL(s), где L(s) = (T1s+1)(T2s +1)(T3s+1). Характеристическое уравнение замкнутой системы будет D(s) = K+L(s)s = b0s4 +b}s3 +b2s2 +b3s + b4 =0, где при заданных из таблицы исходных данных числовых значениях Т1 и Т3 коэффициенты bj будут зависеть от параметров К и Т2. Применение критерия Гурвица к характеристическому уравнению четвертого порядка дает следующие условия устойчивости:
b3(b1b2-b0b3)-b4b12 > 0, b, > 0, i = 0, .,4.
Приравнивая в написанных соотношениях правые части нулю, найдем зависимость К от Т2 и построим в плоскости К и Т2 границы устойчивости, ограничивающие некоторую область устойчивости. При заданном параметре Т2 находим граничное значение КГР коэффициента передачи К.
![]()
К = К1К2К3
b0=![]() =0,165
=0,165![]() =с0
=с0![]()
![]() 5,033
5,033![]() с0
с0
![]()
b3=1 b4=K
Выразим К через параметр Т2:
![]()
Зависимость К(Т2) приведена на рис. 1.2
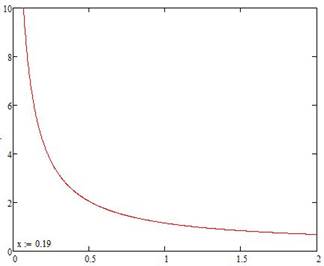
Рис.1.2
Kгр=KT2=0.19=4,633
3.
Полагая К = 0.7КГР, записываем аналитическое выражение для φ(w)= argW(jw), L(w) = 20lg|W(jw)| из W(s) при s = jw.
К=0.7Кгр= 3,243
Передаточную функцию разомкнутой системы можно записать в виде:
![]()
![]()
где
![]()
![]()
тогда:
![]()
![]()
где
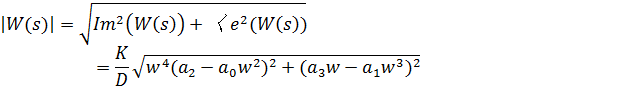
Строим графики логарифмических характеристик разомкнутой системы, с помощью MATLAB (оператор bode или margin) Рис. 1.3 а.
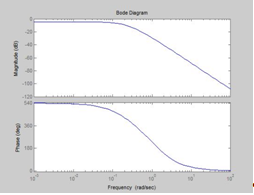
Рис. 1.3а
Строим график АФЧХ с помощью MATLAB (оператор nyquist) рис. 1.3 б для разомкнутой системы.
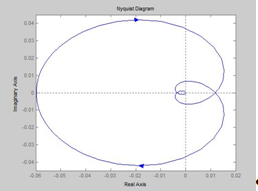
Рис 1.3 б
Запасы устойчивости по модулю и фазе определяются по логарифмическим характеристикам (см. рис. 1.3 а): на частоте среза wс определяется запас по фазе —∆φ, а запас по амплитуде ∆L - на частоте при которой φ(w) = -180. Таким образом, ∆L≈0. 1дБ, ∆φ≈ 0°, что является недостаточным.
4
. Величина ошибки по скорости определяется как eск=V1/K. Для ориентировочной оценки tпп и σ следует построить переходной процесс h(t) (оператор step в MATLAB) при v(t) = 1 и по нему определить tпп и σ.
Для получения уравнений состояний в нормальной форме используем дифференциальное уравнение замкнутой системы
D(s)y(t)=Kv(t). Если D(s)=b0s4+b1s3+b2s2+b3s+b4=0, ,то уравнение состояния имеет вид
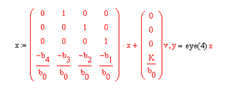
Для описания динамических систем в пространстве состояний в Matlab применяются модели подкласса ss, которые основаны на линейных дифференциальных или разностных уравнениях.
Модель непрерывной системы в подклассе ss имеет вид: Перейти на страницу: 1 2 3 4
Другое по теме:
Проектирование локальной вычислительной сети для организации Коммерческий банк Настоящее техническое задание распространяется на разработку и испытание ЛВС организации «Коммерческий банк», предназначенной для взаимодействия между сотрудниками банка, обмена, передачи информации и для совместного использования периферийного ...