После преобразований и возврата к старым переменным получим:
![]()
![]()
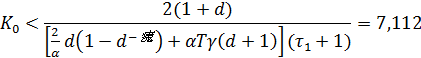
Получим 0<К0<7,112. Таким образом, принимаем К0=0.5 К0’=3,56.
1.
Для построения частотных и логарифмических частотных характеристик в выражении W* (z) делаем замену переменной
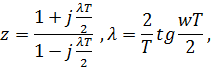
В результате этого получим частотную характеристику W*(jλ) и далее логарифмическую амплитудно-частотную характеристику L*(λ) = 20Lg|W*(jλ)| и фазочастотную характеристику φ*(λ)= argW*(jλ), графики которых строятся в логарифмическом масштабе.
Передаточная функция разомкнутой системы имеет вид
![]()
Тогда можно воспользоваться следующей последовательностью команд в MATLAB:
>> sys=tf(,,1)
Transfer function:
0.231 z + 0.085
---------------------
z^2 - 1.369 z + 0.369
>> sys_tr=d2c(sys,'tustin')
Transfer function:
-0.05332 s^2 - 0.1242 s + 0.4616
--------------------------------
s^2 + 0.9218 s + 2.047e-016
(опция 'tustin’ предназначена для преобразования 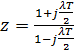 )
)
Получаем выражение:
![]()
где параметры g и f видны из вышеприведенного выражения.
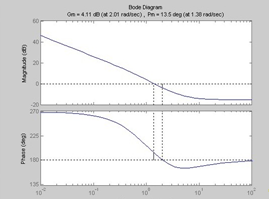
Рис 2.2
4.
Рассматриваемая система для всех вариантов является астатической с астатизмом первого порядка и имеет следующую передаточную функцию:
![]()
![]()
В силу астатизма первого порядка в такой системе статическая ошибка всегда равна нулю, а скоростная еск вычисляется по формуле:
![]()
и следовательно, еск=1,999.
Вычислим коэффициенты ошибок. Величина С0 =0, а коэффициент ошибки
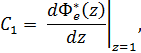
Где ![]() передаточная функция системы по ошибке.
передаточная функция системы по ошибке.
Тогда получим производную:
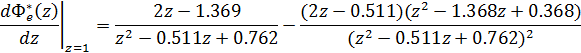
Подставив в последнее выражение найденные ранее значения и z=1, окончательно получим С1=1,999.
5. При входном воздействии вида v(k) = l переходный процесс в замкнутой системе можно вычислить с помощью моделирования импульсной системы в Matlab. Для этого необходимо задать передаточную функцию непрерывной части системы в tf- или zpk -форме, преобразовать ее в дискретную с помощью оператора c2d при заданном времени дискретизации T, а затем построить переходной процесс системы оператором step. Так же можно построить и логарифмические частотные характеристики импульсной системы -bode. Если задана передаточная функция замкнутой системы в виде:
![]()
и периодом дискретизации γT, то получим
>> w0=tf(,) Transfer function:
0.1 s^2 + s
-------------------
0.1 s^2 + s + 3.738
0.2
>> w1=c2d(w0,0.24)
Transfer function:
z^2 - 0.8801 z - 0.1199
------------------------
z^2 - 0.4001 z + 0.09072
Sampling time: 0.24
>> step(W1)

Рис 2.3
На рис.2.4 представлена диаграмма Боде исследуемой дискретной системы с отмеченными на ней запасами устойчивости по амплитуде и фазе.

Рис. 2.4 Перейти на страницу: 1 2
Другое по теме:
Разработка нижнего контура управления змееподобного робота В настоящее время всё чаще требуются мобильные роботы для работы в труднодоступных местах. Для этих целей создано множество роботов и ещё больше разрабатывается. Долгое время основным средством передвижения роботов являлись колесные ил ...