1.4.3 Определение оценок прямых ПК
Выражение для построения вещественной частотной характеристики (ВЧХ) системы по выходу ДОС (рис. 1.19):
.
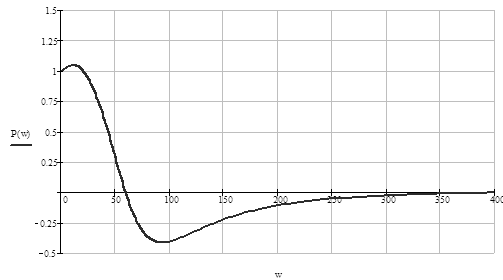
Рис. 1.19. ВЧХ по выходу ДОС
По графику ВЧХ замкнутой системы можно оценить прямые ПК
1. Оценка перерегулирования.
В данном случае график 
имеет положительный максимум и отрицательный минимум. Тогда верхняя оценка перерегулирования:
,
где 
– положительный максимум ВЧХ;
– отрицательный минимум ВЧХ;
– начальное значение ВЧХ.
Следовательно: 
.
2. Оценка времени регулирования.
Время регулирования находится в пределах:
,
где 
– частота положительности.
Тогда: 
.
Выражения для построения ЛАЧХ и ЛФЧХ замкнутой системы по выходу ДОС (рис. 1.20):
,
,
.
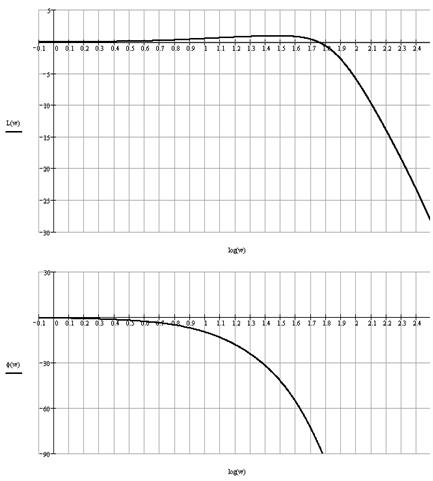
Рис. 1.20. ЛЧХ замкнутой системы по выходу ДОС
1.4.4 Определение корневых оценок прямых ПК
Оценить прямые ПК можно также по корням ПФ ЗС:
.
Нули передаточной функции – корни полинома числителя:
.
Полюса передаточной функции – корни полинома знаменателя:
,
,
,
,
,
.
Изобразим нули и полюса на комплексной плоскости (рис. 1.21).
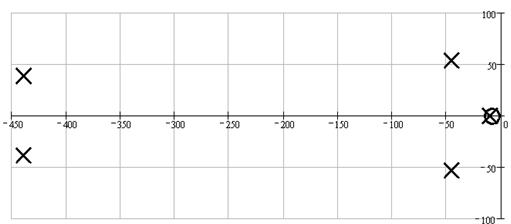
Рис. 1.21. АФЧХ разомкнутой системы
Чтобы оценить прямые ПК необходимо определить доминирующие полюса. Близко расположенные нуль и полюс компенсируют друг друга. Полюс, скомпенсированный нулем, не участвует в оценке прямых ПК. Если выполняется хотя бы одно из неравенств критерия «близости», то нуль компенсирует полюс:
,
.
Проверим выполнение критерия «близости» нуля и полюса :
,
. Перейти на страницу: 1 2 3 4 5
Другое по теме:
Программирование микроконтроллеров Актуальность темы. Микроконтроллеры используются во всех сферах жизнедеятельности человека, устройствах, которые окружают его. Простота подключения и большие функциональные возможности. С помощью программирования микроконтроллера можно решить мн ...