Так как годограф системы, имеющей четвертый порядок, при изменении ω от 0 до ∞, начинается на вещественной положительной полуоси и при увеличении ω в положительном направлении последовательно проходит четыре квадранта, и при этом не обращается в 0, то можно сделать вывод, что замкнутая система устойчива.
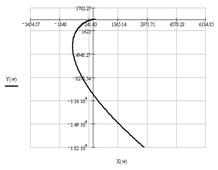
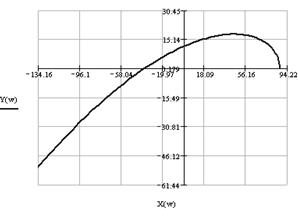Рис. 1.10. Годограф Михайлова (справа увеличен вблизи начала координат)
1.2.3 Определение показателей качества
1. Частота среза разомкнутой системы.
Частота среза разомкнутой системы была определена в анализе системы по критерию Найквиста с использованием ЛЧХ (см. п.1.2.2):
.
2. Запасы устойчивости.
Запасы устойчивости по амплитуде и по фазе определяются по формулам:
, 
,
где 
, 
,
и 
– ЛЧХ разомкнутой системы (см. п.1.2.2):
дБ, 
град.
3. Критический коэффициент усиления системы.
Коэффициент 
определим по алгебраическому критерию Гурвица (см. п.1.1).
ХУЗС: 
,
,
,
,
; 
; 
; 
; 
.
Условие нахождения системы на границе устойчивости:
,
,
.
4. Прямые показатели качества.
Прямые показатели качества системы определяются по графику переходной характеристики замкнутой системы по выходу ДОС Запишем выражение и построим график (рис. 1.11):
.
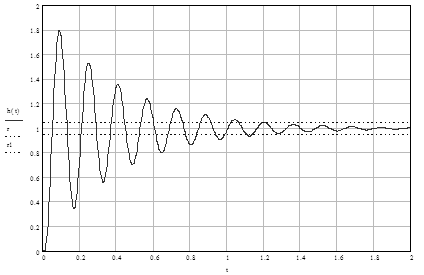
Рис. 1.11. Переходная характеристика замкнутой системы по выходу ДОС
Перерегулирование определяется по формуле:
,
где hmax= 1,793 – максимальное значение переходной характеристики;
hуст= 1 – установившееся значение переходной характеристики; Перейти на страницу: 1 2 3 4 5
Другое по теме:
Проектирование беспроводной сети Wi-Fi Во всем мире стремительно растет потребность в беспроводных соединениях, особенно в сфере бизнеса и IT технологий. Пользователи с беспроводным доступом к информации всегда и везде могут работать гораздо более производительно и эффективно, ч ...